ГОС

Материал из eSyr's wiki.

(Различия между версиями)
Перейти к: навигация, поиск
(→Решение линейного однородного дифференциального уравнения с постоянными коэффициентами)
(→Гармонический ряд)
Строка 34: Строка 34:
=== Гармонический ряд ===
=== Гармонический ряд ===
Доказать расходимость гармонического ряда:
Доказать расходимость гармонического ряда:
-
<math>\sum_{n=0}^\infty \frac{1}{n}</math>
+
<math>\sum_{n=1}^\infty \frac{1}{n}</math>
Покажем по Критерию Коши:
Покажем по Критерию Коши:

Версия 16:15, 7 июня 2010

Содержание

Пределы

Wolfram: lim_{n->infty} (sqrt(n^2+n)-n)

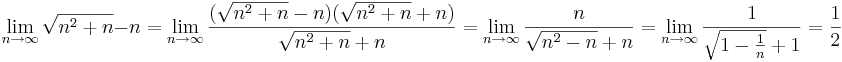
\lim_{n \to \infty} \sqrt{n^2 + n} - n = \lim_{n \to \infty} \frac{(\sqrt{n^2 + n} - n)(\sqrt{n^2 + n} + n)}{\sqrt{n^2 + n} + n} = \lim_{n \to \infty} \frac{n}{\sqrt{n^2 - n}+n} = \lim_{n \to \infty} \frac{1}{\sqrt{1 - \frac{1}{n}}+1} = \frac{1}{2}

Интегралы

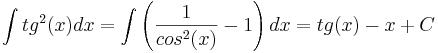
\int tg^2(x) dx = \int \left(\frac{1}{cos^2(x)} - 1\right) dx = tg(x) - x + C

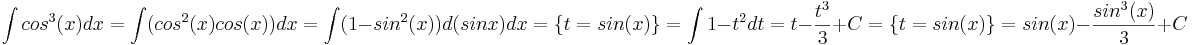
\int cos^3(x) dx = \int (cos^2(x)cos(x)) dx = \int (1 - sin^2(x)) d(sinx) dx = \{t = sin(x)\} = \int 1-t^2 dt = t - \frac{t^3}{3} + C = \{t = sin(x)\} = sin(x)-\frac{sin^3(x)}{3} + C

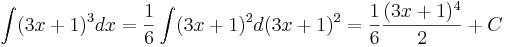
\int (3x + 1)^3 dx = \frac{1}{6} \int (3x + 1)^2d(3x + 1)^2 = \frac{1}{6} \frac{(3x + 1)^4}{2} + C

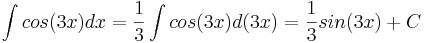
\int cos(3x) dx = \frac{1}{3} \int cos(3x)d(3x) = \frac{1}{3}sin(3x) + C


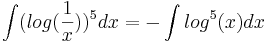
\int (log(\frac{1}{x}))^5 dx = - \int log^5(x)dx

Считаем используя правило:

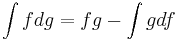
\int fdg = fg - \int g df

f = log5(x)

dg = dx

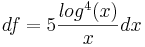
df = 5\frac{log^4(x)}{x} dx


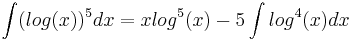
\int (log(x))^5 dx = xlog^5(x) - 5\int log^4(x)dx

Ряды

Гармонический ряд

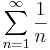
Доказать расходимость гармонического ряда: \sum_{n=1}^\infty \frac{1}{n}

Покажем по Критерию Коши:

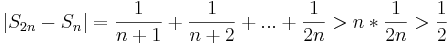
|S_{2n} - S_{n}| = \frac{1}{n+1} + \frac{1}{n+2} + ... + \frac{1}{2n} > n*\frac{1}{2n} > \frac{1}{2}

Не выполняется, если взять 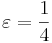\varepsilon = \frac{1}{4}

Так как критерий Коши это необходимое и достаточное условие, то делаем вывод о расходимости ряда.

Знакопеременные ряды

Исследовать на абсолютную и условную сходимость ряд 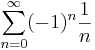\sum_{n=0}^\infty (-1)^n\frac{1}{n}

Здесь можно воспользоваться признаком Лейбница, который говорит, что ряд если an = ( − 1)nbn,an > = 0 и bn монотонно стремится к 0, начиная с некоторого номера n0, то ряд 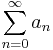\sum_{n=0}^\infty a_n сходится

Последовательность 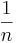\frac{1}{n} монотонно стремится к 0, поэтому по признаку Лейбница 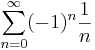\sum_{n=0}^\infty (-1)^n\frac{1}{n} сходится.

Но модуль этого ряда -- это гармонический ряд (то есть расходится). Поэтому сходимость исследуемого ряда условная.

Решение линейного однородного дифференциального уравнения с постоянными коэффициентами

y''' + 2y''' − y' − 2y = 0 (1)

Решение этого уравнения ищется в виде y = eλt

Подставляем этот y в уравнение (1), сокращаем на eλt. Получаем характеристическое уравнение:

λ3 + 2 * λ2 − λ − 2 = 0

Находим корни этого уравнения: λ = 1,λ = − 2,λ = − 1

y1 = et,

y2 = e − 2t,

y3 = e − t


Решение уравнения (1) -- это линейная комбинация yi,i = 1,2,3:

y = C1y1 + C2y2 + C3y3

Получено с http://esyr.me/wiki/%D0%93%D0%9E%D0%A1
Личные инструменты
Разделы