ПОД: Ответы2

Материал из eSyr's wiki.

Перейти к: навигация, поиск

Содержание

Конвейерная обработка данных.

Что необходимо для сложения двух вещественных чисел, представленных в форме с плавающей запятой? Целое множество мелких операций таких, как сравнение порядков, выравнивание порядков, сложение мантисс, нормализация и т.п. Процессоры первых компьютеров выполняли все эти "микрооперации" для каждой пары аргументов последовательно одна за одной до тех пор, пока не доходили до окончательного результата, и лишь после этого переходили к обработке следующей пары слагаемых.

Идея конвейерной обработки заключается в выделении отдельных этапов выполнения общей операции, причем каждый этап, выполнив свою работу, передавал бы результат следующему, одновременно принимая новую порцию входных данных. Получаем очевидный выигрыш в скорости обработки за счет совмещения прежде разнесенных во времени операций. Предположим, что в операции можно выделить пять микроопераций, каждая из которых выполняется за одну единицу времени. Если есть одно неделимое последовательное устройство, то 100 пар аргументов оно обработает за 500 единиц. Если каждую микрооперацию выделить в отдельный этап (или иначе говорят - ступень) конвейерного устройства, то на пятой единице времени на разной стадии обработки такого устройства будут находится первые пять пар аргументов, а весь набор из ста пар будет обработан за 5+99=104 единицы времени - ускорение по сравнению с последовательным устройством почти в пять раз (по числу ступеней конвейера).

Казалось бы конвейерную обработку можно с успехом заменить обычным параллелизмом, для чего продублировать основное устройство столько раз, сколько ступеней конвейера предполагается выделить. В самом деле, пять устройств предыдущего примера обработают 100 пар аргументов за 100 единиц времени, что быстрее времени работы конвейерного устройства! В чем же дело? Ответ прост, увеличив в пять раз число устройств, мы значительно увеличиваем как объем аппаратуры, так и ее стоимость. Представьте себе, что на автозаводе решили убрать конвейер, сохранив темпы выпуска автомобилей. Если раньше на конвейере одновременно находилась тысяча автомобилей, то действуя по аналогии с предыдущим примером надо набрать тысячу бригад, каждая из которых (1) в состоянии полностью собрать автомобиль от начала до конца, выполнив сотни разного рода операций, и (2) сделать это за то же время, что машина прежде находилась на конвейере. Представили себестоимость такого автомобиля? Нет? Согласен, трудно, разве что Ламборгини приходит на ум, но потому и возникла конвейерная обработка... [1]

Оригинальная версия

Длительность арифметической операции может быть уменьшена за счет временного перекрытия ее различных фаз, путем конвейеризации вычислительной работы. Для этого механизмы Арифметического Логического Устройства (АЛУ) выполняется по конвейерному принципу. Пусть, работа АЛУ - для сложении данных, разделена на три этапа, на три автономных блока Рi : Р1 - выравнивание порядков операндов, Р2 - операция сложения мантисс, Р3 - нормализация результата, каждый из ко¬торых выполняется за один условный такт вычислителя. И пусть на таком АЛУ выполняются вычисления: 

 A1 = B1+C1
 A2 = B2+C2
 A3 = B3+C3
 A4 = B4+C4

Тогда временная диаграмма работы АЛУ имеет вид: 

Устройство          1 такт          2 такт        3 такт    4 такт    5 такт            6 такт
P1                  B1+C1            В2+C2	   B3+C3     B4+C4     нет работы       нет работы
P2                 нет работы        B1+C1	   B2+C2     B3+C3     B4+C4            нет работы
P3                 нет работы      нет работы     B1+C1     B2+C2     B3+C3              В4+С4

Вычисления будут выполнены за 6 тактов работы вычислителя, причем, здесь, только два такта работы оборудование было загружено полностью.

ВОПРОС !!!! За сколько тактов будет выполнены эти вычисления, если АЛУ не конвейеризовано? Сокращает ли конвейеризация время выполнения отдельной операции? Спойлер: 12. Нет.

Оптимальную загрузку конвейерных АЛУ можно получить при работе с регулярными структурами, например, при поэлементном сложении векторов. В общем случае, пусть работа операционного блока разбивается на n последовательных частей (стадий, выполняемые за одинаковое время), на которых вычислительные операции выполняются в конвейерном режиме. Тогда, если на выполнение одной операции сложения блоку требуется время T, то на обработку N операций сложения время: Tn = (n + N) * (Т / n). Следовательно, если n << N, то , то ускорение вычислений будет в n раз. Фактором, снижающим производительность конвейеров, явля¬ется конфликты по данным. Так вычисления: 

Вычисления           другая форма этих вычислений
A1 = B1+C1
A2 = A1+C2	        A2 = (B1+C1)+ C2
A3 = B3+C3	        A3 = B3+C3
A4 = B4+C4	        A4 = B4+C4

для правильной работы будут выполняться на два такта дольше: 

Устр.  1такт  2такт   3такт  4такт    5такт   6такт    7такт     8такт
P1	B1+C1   н/р    н/р   A1+C2     B3+C3   B4+C4     н/р       н/р
P2	н/р   B1+C1    н/р     н/р     A1+C2   B3+C3    B4+C4      н/р
P3	н/р     н/р   B1+C1    н/р       н/р   A1+C2    B3+C3     В4+С4

На этой диаграмме видно, что количество простаивающих тактов работы оборудования “н/р” – “конвейерных пузырей “ (pipeline bubble) стало больше.

Внеочередное выполнение команд.

Положив в буфер команды, проводим анализ зависимостей и пытаемся загрузить конвейер теми операциями, которые не зависят от предыдущих (это делает процессор).

Пример:
A1 = B1+C1
A2 = A1+C2
A3 = B3+C3
A4 = B4+C4
8 тактов.

Устр.  1такт  2такт  3такт  4такт    5такт   6такт  7такт      8такт
P1	B1+C1   н/р    н/р   A1+C2    B3+C3   B4+C4   н/р        н/р
P2	н/р   B1+C1    н/р     н/р    A1+C2   B3+C3   B4+C4      н/р
P3	н/р     н/р   B1+C1    н/р     н/р    A1+C2   B3+C3     В4+С4

А вместо этого:
A1 = B1+C1
A3 = B3+C3
A4 = B4+C4
A2 = A1+C2
6 тактов. 

Устр.  1такт  2такт  3такт   4такт    5такт    6такт 
P1	B1+C1  B3+C3   B4+C4   A1+C2    B3+C3   B4+C4   
P2	н/р    B1+C1   B3+C3   B4+C4    A1+C2   B3+C3   
P3	н/р     н/р    B1+C1   B3+C3    В4+С4   A1+C2

Механизмы: Статические и Динамические.

Динамические основаны на оборудовании, которое производит анализ программы и делает преобразования (работа возлагается на процессор).

Статические. Зная архитектуру АЛУ, провести статический анализ и в процессе трансляции оптимизировать программу (работа возлагается на компилятор).

Производительность можно повысить, сделав АЛУ многофункциональным. Если сделать отдельные функциональные элементы для сложения, вычитания, умножения и деления, то схемы становятся проще, а система будет работать быстрее.

Производительность конвейеров.

на intuit.ru

Время выполнения отдельной скалярной операции на конвейерном вы-числителе равно: Т = S + K, где K - время работы, за которое конвейер выдает очередной результат, а S - время запуска конвейера, время заполнения конвейера, которое без учета времени подготовки операндов, равно: S = K*(m-1), где m - число ступеней конвейера. Производительность конвейерного вычислителя на скалярных операциях (число результатов, выдаваемых за единицу времени) равна: R = 1/(S + K).

Время выполнения векторной операции на конвейерном вычислителе равно: Т = S + K*N, где N - длина вектора. Производительность конвейерного вычислителя при векторной работе (число результатов, выдаваемых за единицу времени) равна: R = N/(S + K*N), асимптотическая производительность Rб = 1/K.

Например, при К = 10 нс, Rб = 10^8 результатов/сек, т.е. 100 мегафлопов. Графики достижения такой производительности для S = 100 нс. и S= 1000 нс. показывают, что они имеют различное расстояние до асимптоты. Для оценки этого эффекта используется величина N1/2, определяемая как длина вектора, для которой достигается половина асимптотыческой зависимости. Для приведенного выше примера N1/2 = 100 для S =1000 и N1/2 = 10 для S = 100.

Векторно-конвейерные вычислители.

на intuit.ru

Реализация команд организации цикла (счетчик и переход) при регулярной работе с данными - накладные расходы и препятствие опережающему просмотру на обычных, скалярных вычислителях, показывает, что такие вычисления эффективнее выполнять на специализированном векторно-конвейерном вычислителе.

Если вместо цикла: 

DO L=1,N  
  A(I) = B(I)+C(I)  
ENDDO

использовать запись алгоритма в виде векторной команды сложения вида: 

VADD(B,C,A,N),

то векторный вычислитель, выполняющий такие команды, будет вырабатывать результаты на каждом такте. В таком вычислителе имеется один (или небольшое число) конвейерный процессор, выполняющий векторные команды путем засылки элементов векторов в конвейер с интервалом, равным длительности прохождения одной стадии обработки. Скорость вычислений зависит только от длительности стадии и не зависит от задержек в процессоре в целом.

Так как конвейер для однотипных операций дешевле и быстрее чем для многофункциональных, то выгодно их делать специализированными - однофункциональным: например, только для + или только для *. Для их совместного работы используется принцип зацепления конвейеров. Так, в ЭВМ Крей-1 имеется 12 конвейеров, из них 8 могут быть зацеплены, то есть результаты вычисления конвейера могут быть входными аргументами для другого. Операнды (результаты) находятся в памяти верхнего уровня или на регистрах. Для операндов задается: базовый адрес вектора, число элементов, тип данных в каждом элементе, схема хранения вектора в памяти. Некоторые векторные машины могут работать с двух-трех мерными массивами.

Конвейерная обработка команд.

Команду можно разделить на 6 отрезков:

  • Принять команду
  • Дешифровать КОП
  • Сформировать исполнительный адрес
  • Выбрать операнды
  • Выполнить комманду
  • Записать результат

Конвейерные конфликты.

на intuit.ru

Значительное преимущество конвейерной обработки перед последовательной имеет место в идеальном конвейере, в котором отсутствуют конфликты и все команды выполняются друг за другом без перезагрузки конвейера. Наличие конфликтов снижает реальную производительность конвейера по сравнению с идеальным случаем.

Конфликты - это такие ситуации в конвейерной обработке, которые препятствуют выполнению очередной команды в предназначенном для нее такте.

Конфликты делятся на три группы:

  • структурные,
  • по управлению,
  • по данным.

Структурные конфликты

Структурные конфликты возникают в том случае, когда аппаратные средства процессора не могут поддерживать все возможные комбинации команд в режиме одновременного выполнения с совмещением.

Причины структурных конфликтов.

1. Не полностью конвейерная структура процессора, при которой некоторые ступени отдельных команд выполняются более одного такта. Эту ситуацию можно было бы ликвидировать двумя способами. Первый предполагает увеличение времени такта до такой величины, которая позволила бы все этапы любой команды выполнять за один такт. Однако при этом существенно снижается эффект конвейерной обработки, так как все этапы всех команд будут выполняться значительно дольше, в то время как обычно нескольких тактов требует выполнение лишь отдельных этапов очень небольшого количества команд. Второй способ предполагает использование таких аппаратных решений, которые позволили бы значительно снизить затраты времени на выполнение данного этапа (например, использовать матричные схемы умножения). Но это приведет к усложнению схемы процессора и невозможности реализации на этой БИС других, функционально более важных, узлов. Обычно разработчики процессоров ищут компромисс между увеличением длительности такта и усложнением того или иного устройства процессора.

2. Недостаточное дублирование некоторых ресурсов.

Одним из типичных примеров служит конфликт из-за доступа к запоминающим устройствам.

Борьба с конфликтами такого рода проводится путем увеличения количества однотипных функциональных устройств, которые могут одновременно выполнять одни и те же или схожие функции. Например, в современных микропроцессорах обычно разделяют кэш-память для хранения команд и кэш-память данных, а также используют многопортовую схему доступа к регистровой памяти, при которой к регистрам можно одновременно обращаться по одному каналу для записи, а по другому - для считывания информации. Конфликты из-за исполнительных устройств обычно сглаживаются введением в состав микропроцессора дополнительных блоков. Так, в микропроцессоре Pentium-4 предусмотрено 4 АЛУ для обработки целочисленных данных. Процессоры, имеющие в своем составе более одного конвейера, называются суперскалярными.

Следовательно, для обеспечения правильной работы суперскалярного микропроцессора при возникновении затора в одном из конвейеров должны приостанавливать свою работу и другие. В противном случае может нарушиться исходный порядок завершения команд программы. Но такие приостановки существенно снижают быстродействие процессора. Разрешение этой ситуации состоит в том, чтобы дать возможность выполняться командам в одном конвейере вне зависимости от ситуации в других конвейерах. Это приводит к неупорядоченному выполнению команд. При этом команды, стоящие в программе позже, могут завершиться ранее команд, стоящих впереди. Аппаратные средства микропроцессора должны гарантировать, что результаты выполненных команд будут записаны в приёмник в том порядке, в котором команды записаны в программе. Для этого в микропроцессоре результаты этапа выполнения команды обычно сохраняются в специальном буфере восстановления последовательности команд. Запись результата очередной команды из этого буфера в приемник результата проводится лишь после того, как выполнены все предшествующие команды и записаны их результаты.

По управлению

Конфликты по управлению возникают при конвейеризации команд переходов и других команд, изменяющих значение счетчика команд.

Решения - спекулятивное исполнение, статическое или динамическое предсказание переходов. См. в соотв. секциях.

По данным

Конфликты по данным возникают в случаях, когда выполнение одной команды зависит от результата выполнения предыдущей команды. См. вопрос про Внеочередное выполнение команд.

Спекулятивное выполнение команд.

на intuit.ru

В конвейерных архитектурах устройство выборки команд является таким же конвейером, как и другие функциональные устройства. Так, для условного оператора: 

  IF (A<B)  
    GOTO L;
  S1;
L: S2

еще до вычисления значения условного выражения А<В необходимо решать задачу о заполнении кон¬вейера команд кодами S1 или S2 – спекулятивного выполнения программы (чтобы не было пропуска тактов конвейера из за неверно выбранной ветки, коды которой потребуется убирать из конвейера).

Тривиальное решение состоит в выборе кода, текстуально следующего за командой условного перехода. Для такого оборудования компиляторы могут формировать объектный код с размещением наиболее вероятно выполняемого фрагмента программы непосредственно за командой условного перехода. Так, для циклических конструкций, вероятность перехода на повторение цикла выше вероятности выхода из него. Некоторые системы программирования дают возможность программисту указывать вероятность перехода по метке в условном переходе.

Аппаратный механизм учета вероятности перехода состоит из блока предсказания переходов. Этот блок, кроме (вместо) статически определенных предпочтений для ветвлений, имеет таблицу переходов, в которой хранится история переходов для каждого (в рамках объема таблицы) перехода программы. Большинство современных микропроцессоров обещают точ¬ность предсказаний переходов этим способом выше 90%. Причина повышенного внимания к этому вопросу обусловлена большими задержками, возникающими при неверном предсказании переходов, что грозит существенной потерей производительности. Используемые в микропроцессо¬рах методы предсказания переходов, как уже было сказано, бывают статические и динамические. Как динамический, так и статический подходы имеют свои преимущества и недостатки.

Статическое предсказание условных переходов.

Статические методы предсказания используются реже. Такие предска¬зания делаются компилятором еще до момента выполнения программы. Соответствующие действия компилятора можно считать оптимизацией программ. Такая оптимизация может основываться на сборе информации, получаемой при тестовом прогоне программы (Profile Based Optimisation, PBO) или на эвристических оценках. Результатом деятельности компилятора являются "советы о направлении перехода", помещаемые непосредственно в коды выполняемой программы. Эти советы использует затем аппаратура во время выполнения. В случае, когда переход происходит, или наоборот - как правило, не происходит, советы компилятора часто бывают весьма точны, что ведет к отличным результатам. Преимущество статического подхода - отсутствие необходимости интегрировать на чипе дополнительную аппаратуру предсказания переходов.

Механизмы динамического предсказания переходов.

Большинство производителей современных микропроцессоров снабжают их различными средствами динамического предсказания переходов, производимого на базе анализа "предыстории". Тогда аппаратура собирает статистику переходов, которая помещается в таблицу истории переходов BHT (Branch History Table).В обоих случаях компилятор не может выработать эффективные рекомендации на этапе трансляции программы. В то же время схемы динамического предсказания переходов легко справля¬ются с такими задачами. В этом смысле динамическое предсказание переходов "мощнее" статического. Однако у динамического предсказания есть и свои слабые места - это проблемы, возникающие из-за ограниченности ресурсов для сбора статистики.

Обработка условных операторов в EPIC.

Важной особенностью EPIC-архитектуры является возможность параллельного ветвления в двух случаях: при выполнении команд условного перехода и при выполнении конструкций if-then-else в составе арифметических операторов. Условный переход в "традиционном" исполнении грозит остановкой конвейера. В EPIC-архитектуре предусмотрен запуск дополнительного конвейера по команде подготовки перехода за несколько тактов до ветвления. Интенсивное ветвление в выполняемой программе способно привести к лавинообразному запуску дополнительных конвейеров и необходимости статистической оценки достаточного их количества при обосновании средств аппаратной поддержки.

Поэтому второй случай ветвления, осуществляемого внутри линейного участка программы, предпочтителен, хотя также приводит к избыточности оборудования, используемого при вычислениях.

http://www.citforum.ru/hardware/mersed/mersed_30.shtml

Предикация - способ обработки условных ветвлений. Суть этого способа - компилятор указывает, что обе ветви выполняются на процессоре параллельно. Ведь EPIC процессоры должны иметь много функциональных устройств.

Опишем предикацию более подробно. Если в исходной программе встречается условное ветвление (по статистике - через каждые 6 команд), то команды из разных ветвей помечаются разными предикатными регистрами (команды имеют для этого предикатные поля), далее они выполняются совместно, но их результаты не записываются, пока значения предикатных регистров неопределены. Когда, наконец, вычисляется условие ветвления, предикатный регистр, соответствующий "правильной" ветви, устанавливается в 1, а другой - в 0. Перед записью результатов процессор будет проверять предикатное поле и записывать результаты только тех команд, предикатное поле которых содержит предикатный регистр, установленный в 1.

Эволюция системы команд микропроцессоров.

Двумя основными архитектурами набора команд, используемыми компьютерной промышленностью на современном этапе развития вычислительной техники являются архитектуры CISC и RISC.

CISC

Основоположником CISC-архитектуры можно считать компанию IBM с ее базовой архитектурой /360, ядро которой используется с 1964 года и дошло до наших дней, например, в таких современных мейнфреймах как IBM ES/9000.Лидером в разработке микропроцессоров c полным набором команд (CISC – Complete Instruction Set Computer) считается компания Intel со своей серией x86 и Pentium. Эта архитектура является практическим стандартом для рынка микрокомпьютеров.

Для CISC-процессоров характерно:

  • сравнительно небольшое число регистров общего назначения;
  • большое количество машинных команд, некоторые из которых нагружены семантически аналогично операторам высокоуровневых языков программирования и выполняются за много тактов;
  • большое количество методов адресации;
  • большое количество форматов команд различной разрядности;
  • преобладание двухадресного формата команд;
  • наличие команд обработки типа регистр-память.

RISC

Основой архитектуры современных рабочих станций и серверов является архитектура компьютера с сокращенным набором команд (RISC – Reduced Instruction Set Computer). Зачатки этой архитектуры уходят своими корнями к компьютерам CDC6600, разработчики которых (Торнтон, Крэй и др.) осознали важность упрощения набора команд для построения быстрых вычислительных машин. Эту традицию упрощения архитектуры С. Крэй с успехом применил при создании широко известной серии суперкомпьютеров компании Cray Research. Однако окончательно понятие RISC в современном его понимании сформировалось на базе трех исследовательских проектов компьютеров: процессора 801 компании IBM, процессора RISC университета Беркли и процессора MIPS Стенфордского университета.

Среди других особенностей RISC-архитектур следует отметить наличие достаточно большого регистрового файла (в типовых RISC-процессорах реализуются 32 или большее число регистров по сравнению с 8 – 16 регистрами в CISC-архитектурах), что позволяет большему объему данных храниться в регистрах на процессорном кристалле большее время и упрощает работу компилятора по распределению регистров под переменные.

Для обработки, как правило, используются трехадресные команды, что помимо упрощения дешифрации дает возможность сохранять большее число переменных в регистрах без их последующей перезагрузки.

Развитие архитектуры RISC в значительной степени определялось прогрессом в области создания оптимизирующих компиляторов. Именно современная техника компиляции позволяет эффективно использовать преимущества большего регистрового файла, конвейерной организации и большей скорости выполнения команд. Современные компиляторы используют также преимущества другой оптимизационной техники для повышения производительности, обычно применяемой в процессорах RISC: реализацию задержанных переходов и суперскалярной обработки, позволяющей в один и тот же момент времени выдавать на выполнение несколько команд.

Следует отметить, что в последних разработках компании Intel (имеются в виду Pentium и Pentium Pro ), а также ее последователей-конкурентов (AMD R5, Cyrix M1, NexGen Nx586 и др.) широко используются идеи, реализованные в RISC-микропроцессорах, так что многие различия между CISC и RISC стираются. Однако сложность архитектуры и системы команд x86 остается и является главным фактором, ограничивающим производительность процессоров на ее основе.

Суперскалярные микропроцессоры.

Суперскалярный процессор представляет собой нечто большее, чем обычный последовательный (скалярный) процессор. В отличие от последнего, он может выполнять несколько операций за один такт. Основными компонентами суперскалярного процессора являются устройства для интерпретации команд (УУ), снабженные логикой, позволяющей определить, являются ли команды независимыми, и достаточное число исполняющих устройств (ФУ, АЛУ). В исполняющих устройствах могут быть конвейеры. Суперскалярные процессоры реализуют параллелизм на уровне команд. Примером компьютера с суперскалярным процессором является IBM RISC/6000. Тактовая частота процессора у ЭВМ была 62.5 МГц, а быстродействие системы на вычислительных тестах достигало 104 Mflop (Mflop - единица измерения быстродействия процессора - миллион операций с плавающей точкой в секунду). Суперскалярный процессор не требует специальных векторизующих компиляторов, хотя компилятор должен в этом случае учитывать особенности архитектуры. Итак, суперскалярные процессор призван, в отличие от VLIW, динамически определять места распараллеливания

Широкоформатные команды для параллельной обработки данных.

В ЭВМ с архитектурой VLIW (Very Long Instruction Word) - (очень большие командные слова), команды могут иметь широкий формат (длину) и команда может содержать несколько содержательных инструкций, выполнение которых детально регламентируется в терминах тактов работы АУ (параллельное выполнение нескольких команд в АУ). В таких архитектурах имеется возможность программировать вычислительные алгоритмы (включая векторные) с максимальной производительностью для данной аппаратуры. В них вся работа по оптимальному программированию возлагается на системы программирования (или ручное программирование).

Однако упрощения в архитектуре управления приводит к значительному возрастанию сложности задачи планирования выдачи команд, так программными средствами должна быть обеспечена точная синхронизация считывания и записи данных. При этом необходимо так планировать параллельное выполнение операций машины, чтобы выполнялись определенные ограничения на число одновременно считываний и записей в наборы регистров, использование ФУ и т.д. Размер командного слова в машинах данной архитектуры - FPS (AP-120B) - 64 бита, Multilow Tract - 1024.

Определяющие свойства архитектуры VLIW:

  • Одно центральное управляющее устройство, обрабатывающее за один такт одну длинную команду.
  • Большое число функциональных устройств (ФУ) - АЛУ.
  • Наличия в длинной команде полей, каждое из которых содержит команду управления некоторым функциональным устройством или команду обращения к памяти.
  • Статически определенная длительность в тактах исполнения каждой операции. Операции могут быть конвейеризованы.
  • Закрепление во время компиляции банков расслоенной памяти за ФУ для получения максимальной ширины доступа для данных, которые можно соединить в одну команду.
  • Система передвижения данных между ФУ, минуя память. Маршрут передвижения полностью специфицируется во время компиляции.
  • Практическая невозможность ручного программирования в силу большой сложности возникающих комбинаторных задач.

Проект EPIC.

http://www.wl.unn.ru/~ragozin/diff/Itanium.htm

EPIC - Explicitly Parallel Instruction Computing

Архитектура EPIC представляет собой пример научно-исследовательской разработки, представляющей собой скорее принцип обработки информации, нежели архитектуру конкретного процессора. В архитектуре сочетаются многие технологические решения, довольно разнотипные, которые в результате сочетания дают значительное повышение скорости обработки и решение некоторых проблем трансляции программ.

Архитектура EPIC (базовые принципы) были разработаны в университете Иллинойса, проект имел название Impact. В начале 1990-х годов были заложены теоретические основы самой архитектуры, затем были начаты работы в рамках создания инструментальных средств для процессора EPIC. Проект по созданию инструментальных средств известен под названием Trimaran. Архитектура EPIC имеет следующие основные особенности: (мы не будем обсуждать конкретные параметры конвейеров процессора, так как EPIC является в большей степени концептуальной моделью, чем типовым образцом для тиражирования процессоров)

  • поддержка явно выделенного компилятором параллелизма. Формат команд имеет много общего с архитектурой с длинным командным словом - параллелизм так же явно выделен. Однако, если длинное командное слово имеет обычно чётко заданную ширину (хотя в процессорах с нерегулярным длинным командным словом слова могут быть разными), в процессоре EPIC существует некоторое количество образцов длинных команд, в которых функциональным устройствам процессора явно сопоставлена операция. Кроме того, ряд образцов может сопоставлять инструкции из различных тактов выполнения, т.е. инструкция явно выполняется за 1-2 такта, в этом случае в образце инструкции явно специфированы между какими командами имеется слот задержки (фактически "граница" между командами, выполняемыми в разных тактах). К каждой длинной команде (128 бит) прилагается небольшой (3-5 битный) ярлык, который специфицирует формат команды.
  • наличие большого регистрового файла
  • наличие предикатных регистров, подобно архитектуре PowerPC. Предикатные регистры позволяет избавится от известной проблемы с неразделяемым ресурсом регистра флагов большинства процессоров, поддерживающих скалярный параллелизм - программная конвееризация циклов, содержащих условные переходы, практически невозможна. Множественный предикатный флаговый регистр позволяет избавится от паразитных связей по управлению из-за регистра флагов.
  • спекулятивная загрузка данных, позволяющая избежать простоев конвейера при загрузке данных из оперативной памяти
  • поддержка предикатно-выполняемых команд, которая позволяет: 1) избежать излишнихинструкций ветвления, если количество команд в ветвях условного оператора невелико; 2) уменьшить нагрузку на устройство предсказания переходов.
  • аппаратная поддержка програмной конвейеризации с поомшью механизма переименования регистров.
  • Используется стек регистров (и регистровые окна).
  • Для предсказания инструкций используется поддержка компилятора.
  • Имеется специальная поддержка програмной конвейеризации (метод составления расписания команд "по модулю") циклов, когда на каждой итерации имена регистров сдвигаются и каждая новая итерация оперирует уже с новым набором регистров.
  • Введена поддержка инструкций циклического выполнения команд без потерь времени на инструкции циклического выполнения.

Наиболее интересной в архитектуре EPIC является поддержка спекулятивное выполнение команд и загрузка данных. Спекулятивное исполнение команд. Большинство команд загрузки данных из памяти выполняется длительное время. Выполнение команды за 1-2 такта возможно только в том случае, если значение содержится в кеш-памяти второго уровня. Время несколько увеличивается, если значение находится в кеш-памяти второго уровня. В случае чтения же данных из микросхем динамической памяти даже при попадании на активную страницу происходит значительная задержка при загрузке, а при смене страницы задержка имеет астрономическую величину, причём конвейер быстро блокируется, так команд, которые можно выполнить без нарушения зависимости по данным, обычно оказывается крайне мало.

При спекулятивном выполнении используется вынесение команд загрузки далеко вперёд инструкций, использующих эти данные, в основном вверх за инструкции условного перехода. При достижении потоком команд места, где необходимо использовать загружаемые данные, вставляется инструкция, проверяющая не произошло ли исключения в процессе загрузки (например, какая-то инструкция произвела запись по этому адресу), если исключение произошло, то вызывается специально написанный восстановитеьный код, который попросту перезагружает значение в регистр.

При спекулятивных операциях по данным оптимизируется часто встречающийся участок во многих программах. Рассмотрим фрагмент программы: 

int *p,*t;
int a,b;
...
*p = b;
a = *t;

В случае, если компилятор не имеет достаточно информации для проведения анализа потока данных, он не может определить, перекрываются ли области памяти, адресуемые указателями p и t. В этом случае каждый раз значение надо перезагружать, но, мало того, инструкции загрузки нельзя переупорядочить. Для получения возможности переупорядочивания этих инструкций используется спекуляция по данным. Инструкция загрузки переносится наверх, при этом, если произведена запись, затрагивающая загружаемое содержимое, то производится вызов кода восстановления, перезагружающего значение.

Мультитредовые, многоядерные вычислители.

wikipedia:Multithreading

Классификация параллельных вычислителей по Флинну.

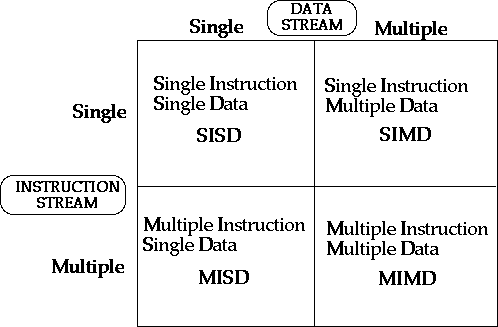
По-видимому, самой ранней и наиболее известной является классификация архитектур вычислительных систем, предложенная в 1966 году М.Флинном. Классификация базируется на понятии потока, под которым понимается последовательность элементов, команд или данных, обрабатываемая процессором. На основе числа потоков команд и потоков данных Флинн выделяет четыре класса архитектур: SISD,MISD,SIMD,MIMD. Эти четыре класса архитектур схематически представляются в виде квадрата, называемого квадратом Флинна.

Изображение:Taxonomy.gif

SISD

SISD (single instruction stream / single data stream) -- одиночный поток команд и одиночный поток данных. К этому классу относятся, прежде всего, классические последовательные машины, или иначе, машины фон-неймановского типа, например, PDP-11 или VAX 11/780. В таких машинах есть только один поток команд, все команды обрабатываются последовательно друг за другом и каждая команда инициирует одну операцию с одним потоком данных. Не имеет значения тот факт, что для увеличения скорости обработки команд и скорости выполнения арифметических операций может применяться конвейерная обработка -- как машина CDC 6600 со скалярными функциональными устройствами, так и CDC 7600 с конвейерными попадают в этот класс.

SIMD

SIMD (single instruction stream / multiple data stream) - одиночный поток команд и множественный поток данных. В архитектурах подобного рода сохраняется один поток команд, включающий, в отличие от предыдущего класса, векторные команды. Это позволяет выполнять одну арифметическую операцию сразу над многими данными - элементами вектора. Способ выполнения векторных операций не оговаривается, поэтому обработка элементов вектора может производится либо процессорной матрицей, как в ILLIAC IV, либо с помощью конвейера, как, например, в машине CRAY-1.

Машины типа SIMD.

Машины типа SIMD состоят из большого числа идентичных процессорных элементов, имеющих собственную память. Все процессорные элементы в такой машине выполняют одну и ту же программу. Очевидно, что такая машина, составленная из большого числа процессоров, может обеспечить очень высокую производительность только на тех задачах, при решении которых все процессоры могут делать одну и ту же работу. Модель вычислений для машины SIMD очень похожа на модель вычислений для векторного процессора: одиночная операция выполняется над большим блоком данных.

В отличие от ограниченного конвейерного функционирования векторного процессора, матричный процессор (синоним для большинства SIMD-машин) может быть значительно более гибким. Обрабатывающие элементы таких процессоров - это универсальные программируемые ЭВМ, так что задача, решаемая параллельно, может быть достаточно сложной и содержать ветвления. Обычное проявление этой вычислительной модели в исходной программе примерно такое же, как и в случае векторных операций: циклы на элементах массива, в которых значения, вырабатываемые на одной итерации цикла, не используются на другой итерации цикла.

Модели вычислений на векторных и матричных ЭВМ настолько схожи, что эти ЭВМ часто обсуждаются как эквивалентные.

MISD

MISD (multiple instruction stream / single data stream) - множественный поток команд и одиночный поток данных. Определение подразумевает наличие в архитектуре многих процессоров, обрабатывающих один и тот же поток данных. Однако ни Флинн, ни другие специалисты в области архитектуры компьютеров до сих пор не смогли представить убедительный пример реально существующей вычислительной системы, построенной на данном принципе. Ряд исследователей [3,4,5] относят конвейерные машины к данному классу, однако это не нашло окончательного признания в научном сообществе. Будем считать, что пока данный класс пуст.

MIMD

MIMD (multiple instruction stream / multiple data stream) - множественный поток команд и множественный поток данных. Этот класс предполагает, что в вычислительной системе есть несколько устройств обработки команд, объединенных в единый комплекс и работающих каждое со своим потоком команд и данных.

Машины типа MIMD.

Термин "мультипроцессор" покрывает большинство машин типа MIMD и (подобно тому, как термин "матричный процессор" применяется к машинам типа SIMD) часто используется в качестве синонима для машин типа MIMD. В мультипроцессорной системе каждый процессорный элемент (ПЭ) выполняет свою программу достаточно независимо от других процессорных элементов. Процессорные элементы, конечно, должны как-то связываться друг с другом, что делает необходимым более подробную классификацию машин типа MIMD. В мультипроцессорах с общей памятью (сильносвязанных мультипроцессорах) имеется память данных и команд, доступная всем ПЭ. С общей памятью ПЭ связываются с помощью общей шины или сети обмена. В противоположность этому варианту в слабосвязанных многопроцессорных системах (машинах с локальной памятью) вся память делится между процессорными элементами и каждый блок памяти доступен только связанному с ним процессору. Сеть обмена связывает процессорные элементы друг с другом.

Базовой моделью вычислений на MIMD-мультипроцессоре является совокупность независимых процессов, эпизодически обращающихся к разделяемым данным. Существует большое количество вариантов этой модели. На одном конце спектра - модель распределенных вычислений, в которой программа делится на довольно большое число параллельных задач, состоящих из множества подпрограмм. На другом конце спектра - модель потоковых вычислений, в которых каждая операция в программе может рассматриваться как отдельный процесс. Такая операция ждет своих входных данных (операндов), которые должны быть переданы ей другими процессами. По их получении операция выполняется, и полученное значение передается тем процессам, которые в нем нуждаются. В потоковых моделях вычислений с большим и средним уровнем гранулярности, процессы содержат большое число операций и выполняются в потоковой манере.

Примеры и особенности

Итак, что же собой представляет каждый класс? В SISD, как уже говорилось, входят однопроцессорные последовательные компьютеры типа VAX 11/780. Однако, многими критиками подмечено, что в этот класс можно включить и векторно-конвейерные машины, если рассматривать вектор как одно неделимое данное для соответствующей команды. В таком случае в этот класс попадут и такие системы, как CRAY-1, CYBER 205, машины семейства FACOM VP и многие другие.

Бесспорными представителями класса SIMD считаются матрицы процессоров: ILLIAC IV, ICL DAP, Goodyear Aerospace MPP, Connection Machine 1 и т.п. В таких системах единое управляющее устройство контролирует множество процессорных элементов. Каждый процессорный элемент получает от устройства управления в каждый фиксированный момент времени одинаковую команду и выполняет ее над своими локальными данными. Для классических процессорных матриц никаких вопросов не возникает, однако в этот же класс можно включить и векторно-конвейерные машины, например, CRAY-1. В этом случае каждый элемент вектора надо рассматривать как отдельный элемент потока данных.

Класс MIMD чрезвычайно широк, поскольку включает в себя всевозможные мультипроцессорные системы: Cm*, C.mmp, CRAY Y-MP, Denelcor HEP,BBN Butterfly, Intel Paragon, CRAY T3D и многие другие. Интересно то, что если конвейерную обработку рассматривать как выполнение множества команд (операций ступеней конвейера) не над одиночным векторным потоком данных, а над множественным скалярным потоком, то все рассмотренные выше векторно-конвейерные компьютеры можно расположить и в данном классе.

Предложенная схема классификации вплоть до настоящего времени является самой применяемой при начальной характеристике того или иного компьютера. Если говорится, что компьютер принадлежит классу SIMD или MIMD, то сразу становится понятным базовый принцип его работы, и в некоторых случаях этого бывает достаточно. Однако видны и явные недостатки. В частности, некоторые заслуживающие внимания архитектуры, например dataflow и векторно--конвейерные машины, четко не вписываются в данную классификацию. Другой недостаток - это чрезмерная заполненность класса MIMD. Необходимо средство, более избирательно систематизирующее архитектуры, которые по Флинну попадают в один класс, но совершенно различны по числу процессоров, природе и топологии связи между ними, по способу организации памяти и, конечно же, по технологии программирования.

Наличие пустого класса (MISD) не стоит считать недостатком схемы. Такие классы, по мнению некоторых исследователей в области классификации архитектур [6,7], могут стать чрезвычайно полезными для разработки принципиально новых концепций в теории и практике построения вычислительных систем.

Статические коммутационные сети.

Статические сети имеют жестко фиксированные соединения, вход и выход зафиксированы без возможности переключения. Наиболее простой топологией сети является линейка – одномерная сетка. Для обеспечения передачи информации между несмежными узлам используются транзитные пересылки. Для цепочки из М узлов наиболее медленная пересылка есть пересылка между конечными ПЭ линейки и она потребует (М-1) транзитных пересылок. Число таких пересылок для любой статической топологии сети считается ее параметром и называется – диаметром сети. Если связать конечные ПЭ линейки, то такая топология - кольцо будет иметь меньший диаметр. Сети могут иметь вид: одномерный линейный массив, двумерное кольцо, звезда, сетка и гексагональный массив, дерево, трехмерное пол­ностью связанное хордовое кольцо, 3 -мерный куб, сети из циклически связанных 3-мерных кубов, D - мерный массив с топологией гиперкуба, тасовка (совершенная, обменная). Недостаток - необходимость маршрутизации транзитных сообщений. По топологии гиперкуба, каждое ПЭ связывается со своим ближайшем соседом в n мерном пространстве. У каждого узла в двумерном гиперкубе имеются два ближайших соседа, в трехмерном - три, в четырехмерном - четыре.

Динамические коммутаторы.

Перед нами стоит задача осуществления эффективного управления межсегментным трафиком с целью уменьшения числа критичных участков сети. Статические коммутаторы не смогут удовлетворить всем требованиям. Совсем иначе дело обстоит с динамическими коммутаторами. Эти устройства не только уделяют особое внимание пересылке кадров по предписанному адресу, но и обрабатывают таблицу соответствий отдельных узлов конкретным портами, к которым они подключены. Эта информация обновляется каждый раз, как только очередная машина начинает передачу данных (или же через заранее заданные интервалы времени). Таблица постоянно обновляющихся комбинаций узел/порт предоставляет коммутатору возможность быстро направлять пакеты через соответствующие сегменты. Динамические коммутаторы позволят экономить время и силы в течение еще довольно продолжительного времени. Поскольку эти устройства обновляют свои таблицы соединений каждый раз, когда устройства начинают передачу, можно переупорядочить сеть, переключая рабочие станции на разные порты до тех пор, пока сеть не будет сконфигурирована оптимальным образом. (Учтите, что этим можно заниматься до посинения.) Таблицы будут обновляться автоматически, и сеть будет в полном порядке.

В сетях с динамической коммутацией:

  • разрешается устанавливать соединение по инициативе пользователя сети;
  • коммутация выполняется только на время сеанса связи, а затем (по инициативе одного из пользователей) разрывается;
  • в общем случае пользователь сети может соединиться с любым другим пользователем сети;
  • время соединения между парой пользователей при динамической коммутации составляет от нескольких секунд до нескольких часов и завершается после выполнения определенной работы — передачи файла, просмотра страницы текста или изображения и т.п.

Динамический коммутатор не только повышает пропускную способность, но и увеличивает степень защищенности информации в сети, так как пакеты передаются строго от источника к адресату. Динамические коммутаторы позволяют управлять трафиком в сети, разрешая передачу пакетов только для определенных сочетаний адресов отправителя и получателя. Разрешенные пары адресов образуют виртуальный сегмент, доступ к которому остальным запрещен. Каждая станция может входить в состав нескольких виртуальных сегментов.

Динамические коммутаторы применяются в локальных сетях для повышения пропускной способности. Наиболее явны преимущества динамической коммутации в случае, когда идет постоянное обращение к одному или нескольким высокопроизводительным серверам. Выделение каждому серверу отдельного Switch-порта и подключение к другим портам отдельных сегментов сети позволяет существенно снизить количество коллизий в сети. Другое важное преимущество применения динамических коммутаторов -- это возможность организации виртуальных сетей. У администратора появляется возможность логической конфигурации сети в соответствии с реальными информационными связями без изменения физической коммутации.

Метакомпъютинг.

GRID-сети это совокупность вычислительных систем, связанных через Интернет (метакомпьютинг). Используются для решения задач, допускающих сегментацию на независимые вычислительные процессы с большим объемом вычислений. Такими задачами являются задача исследования генома, обработку результатов физических испытаний, проект CETI.

Основная схема работы в этом случае примерно такая: специальный агент, расположенный на вычислительном узле (компьютере пользователя), определяет факт простоя этого компьютера, соединяется с управляющим узлом метакомпьютера и получает от него очередную порцию работы (область в пространстве перебора). По окончании счета по данной порции вычислительный узел передает обратно отчет о фактически проделанном переборе или сигнал о достижении цели поиска. Далее на данной странице будут вкратце описаны и приведены ссылки на основные исследовательские проекты в области мета-компьютинга, разработанные программные технологии, конкретные примеры мета-компьютеров. Нет централизованного управление, основные архитектуры – Legion (объектно-ориентир), Globus (в терминах предоставления сервисов).

Метакомпьютер может не иметь постоянной конфигурации - отдельные компоненты могут включаться в его конфигурацию или отключаться от нее; при этом технологии метакомпьютинга обеспечивают непрерывное функционирование системы в целом. Современные исследовательские проекты в этой области направлены на обеспечение прозрачного доступа пользователей через Интернет к необходимым распределенным вычислительным ресурсам, а также прозрачного подключения простаивающих вычислительных систем к метакомпьютерам.

Вычислительные кластеры.

Вычислительные кластеры (cluster) – группа ЭВМ (серверов), связанная между собой системной сетью и функционирующая с точки зрения пользователя как единый вычислительный узел. Локальные сети отличаются от кластеров тем, что узлы локальной сети используются индивидуально, в соответствии со своим назначением. В свою очередь кластеры разделяются на Высокоскоростные (High Performance, HP) и Системы Высокой Готовности (High Availability, HA), а также Смешанные Системы.

Высокоскоростные системы предназначены для задач, которые требуют больших вычислительных мощностей: обработка изображений, научные исследования, математическое моделирование и т. д.

Кластеры высокой готовности используются в банковских операциях, электронной коммерции и т д.

Архитектура. Кластер - это набор рабочих станций (или даже ПК) общего назначения, используется в качестве дешевого варианта массивно-параллельного компьютера. Для связи узлов используется одна из стандартных сетевых технологий (Fast/Gigabit Ethernet, Myrinet) на базе шинной архитектуры или коммутатора. При объединении в кластер компьютеров разной мощности или разной архитектуры, говорят о гетерогенных (неоднородных) кластерах. Узлы кластера могут одновременно использоваться в качестве пользовательских рабочих станций. В случае, когда это не нужно, узлы могут быть существенно облегчены и/или установлены в стойку.

Примеры NT-кластер в NCSA, Beowulf-кластеры.

Операционная система Используются стандартные для рабочих станций ОС, чаще всего, свободно распространяемые - Linux/FreeBSD, вместе со специальными средствами поддержки параллельного программирования и распределения нагрузки.

Модель программирования Программирование, как правило, в рамках модели передачи сообщений (чаще всего - MPI). Дешевизна подобных систем оборачивается большими накладными расходами на взаимодействие параллельных процессов между собой, что сильно сужает потенциальный класс решаемых задач.

Матричные параллельные мультипроцессоры.

Архитектура Система состоит из однородных вычислительных узлов (объединенных в матрицы или гиперкубы), включающих:

  • один или несколько центральных процессоров (обычно RISC),
  • локальную память (прямой доступ к памяти других узлов невозможен),
  • коммуникационный процессор или сетевой адаптер
  • иногда - жесткие диски (как в SP) и/или другие устройства В/В

К системе могут быть добавлены специальные узлы ввода-вывода и управляющие узлы. Узлы связаны через некоторую коммуникационную среду (высокоскоростная сеть, коммутатор и т.п.)

Примеры IBM RS/6000 SP2, Intel PARAGON/ASCI Red, CRAY T3E, Hitachi SR8000, транспьютерные системы Parsytec. Масштабируемость Общее число процессоров в реальных системах достигает нескольких тысяч (ASCI Red, Blue Mountain).

Операционная система Существуют два основных варианта:

  • Полноценная ОС работает только на управляющей машине (front-end), на каждом узле работает сильно урезанный вариант ОС, обеспечивающие только работу расположенной в нем ветви параллельного приложения. Пример: Cray T3E.
  • На каждом узле работает полноценная UNIX-подобная ОС (вариант, близкий к кластерному подходу, однако скорость выше, чем в кластере). Пример: IBM RS/6000 SP + ОС AIX, устанавливаемая отдельно на каждом узле.

Модель программирования Программирование в рамках модели передачи сообщений (MPI, PVM, BSPlib)

Симметричные мультипроцессоры.

Системы данного класса: SMP (Scalable Parallel Processor) состоят из нескольких однородных процессоров и массива общей памяти (разделяемой памяти – shared memory): любой процессор может обращаться к любому элементу памяти. По этой схеме построены 2,4 процессорные SMP сервера на базе процессоров Intel, НР и т. д., причем процессоры подключены к памяти с помощью общей шины. Системы с большим числом процессоров (но не более 32) подключаются к общей памяти, разделенной на блоки, через не блокирующийся полный коммутатор: crossbar. Любой процессор системы получает данное по произвольному адресу памяти за одинаковое время, такая структура памяти называется: UMA - Uniform Memory Access (Architecture). Пример:НР-9000. Дальнейшее масштабирование (увеличение числа процессоров системы) SMP систем обеспечивается переходом к архитектуре памяти: NUMA - Nоn Uniform Memory Access. По схеме, называемой, этой иногда, кластеризацией SMP, соответствующие блоки памяти двух (или более) серверов соединяются кольцевой связью, обычно по GCI интерфейсу. При запросе данного, расположенного вне локального с сервере диапазона адресов, это данное по кольцевой связи переписывается дублируется в соответствующий блок локальной памяти, ту часть его, которая специально отводится для буферизации глобальных данных и из этого буфера поставляется потребителю. Эта буферизация прозрачна (невидима) пользователю, для которого вся память кластера имеет сквозную нумерацию, и время выборки данных, не локальных в сервере, будет равно времени выборки локальных данных при повторных обращениях к глобальному данному, когда оно уже переписано в буфер. Данный аппарат буферизации есть типичная схема кэш памяти. Так как к данным возможно обращение из любого процессора кластера, то буферизация, размножение данных требует обеспечение их когерентности. Когерентность данных состоит в том, что при изменении данного все его потребители должны получать это значение. Проблема когерентности усложняется дублированием данных еще и в процессорных кэшах системы. Системы, в которых обеспечена когерентность данных, буферизуемых в кэшах, называются кэш когерентными (cc-cache coherent), а архитектура памяти описываемого кластера: cc- NUMA (cache coherent Nоn Uniform Memory Access). Классической архитектурой принято считать систему SPP1000.

Архитектура памяти cc-NUMA.

cc-NUMA – “неоднородный доступ к памяти с поддержкой когерентности кэшей”. Логически память NUMA системы представляется единым сплошным массивом, но распределена между узлами. Любые изменения сделанные каким-либо процессором в памяти становятся доступны всем процессорам благодаря механизму поддержания когерентности кэшей. Архитектура cc-NUMA предполагает кэширование как вертикальных (процессор - локальная память) так и горизонтальных (узел - узел) связей. Кэширование вертикальных связей позволяет организовать каждый узел как UMA компьютер, позволяя получить преимущества UMA архитектуры используя небольшое количество процессоров (обычно 2 или 4) над общей памятью и увеличивая тем самым производительность до 4 раз. В тоже время, возможность комбинирования в одной вычислительной системе множества узлов UMA данной архитектуры позволяет наращивать мощность, не увеличивая слишком количества процессоров в каждом узле. А это позволяет использовать преимущества UMA архитектур, и одновременно имея большое количество процессоров в одной вычислительной системе.

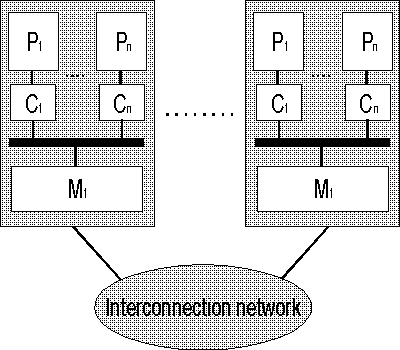
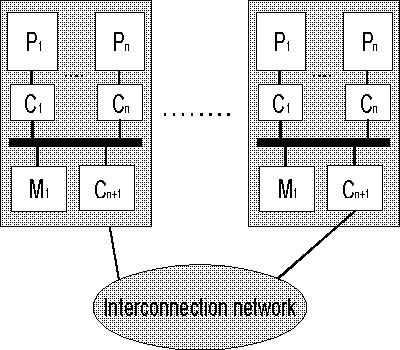
На рисунке ниже представлены различия между NUMA и cc-NUMA архитектурами:

Общая структура архитектуры NUMA

Изображение:Image7-1-.gif

Общая структура архитектуры cc-NUMA.

Изображение:Image8-1-.gif

Обозначения: P – процессор, С – кэш, М – память, Interconnection network – соединяющая сеть.

В системе CC-NUMA физически распределенная память объединяется, как в любой другой SMP-архитектуре, в единый массив. Не происходит никакого копирования страниц или данных между ячейками памяти. Адресное пространство в данных архитектурах делится между узлами. Данные, хранящиеся в адресном пространстве некоторого узла, физически хранятся в этом же узле. Нет никакой программно - реализованной передачи сообщений. Существует просто одна карта памяти, с частями, физически связанными медным кабелем, и очень умные (в большей степени, чем объединительная плата) аппаратные средства. Аппаратно - реализованная кэш-когерентность означает, что не требуется какого-либо программного обеспечения для сохранения множества копий обновленных данных или для передачи их между множеством экземпляров ОС и приложений. Со всем этим справляется аппаратный уровень точно так же, как в любом SMP-узле, с одной копией ОС и несколькими процессорами.

Архитектура cc-NUMA

Парадигмы программирования для параллельных вычислителей.

  • Модель Передачи сообщений. В этой модели процессы независимы и имеют собственное адресное пространство. Основной способ взаимодействия и синхронизации – передача сообщений. Стандарт интерфейса передачи сообщений является MPI.
  • Модель с общей памятью. В этой модели процессы имеют единое адресное пространство. Доступ к общим данным регламентируется с помощью примитивов синхронизации. Стандартом для моделей с общей памятью является OpenMP.
  • Модель параллелизма по данным. В этой модели данные разделяются между узлами вычислительной системы , а последовательная программа их обработки преобразуется компилятором либо в модель передачи сообщений, либо в модель с общей памятью. При этом вычисления распределяются по правилу собственных вычислений: каждый процессор выполняет вычисление данных, распределенных на него. Примерами могут являться стандарты HPF1 HPF2. На модели параллелизма по данным была разработана отечественная система DVM.

Нетрадиционные вычислители.

Графические процессоры

Графический процессор (англ. Graphics Processing Unit, GPU) — отдельное устройство персонального компьютера или игровой приставки, выполняющее графический рендеринг. Современные графические процессоры очень эффективно обрабатывают и изображают компьютерную графику, благодаря специализированной конвейерной архитектуре они намного эффективнее в обработке графической информации, чем типичный центральный процессор.

Графический процессор в современных видеоадаптерах применяется в качестве ускорителя трёхмерной графики, однако его можно использовать в некоторых случаях и для вычислений (GPGPU). Отличительными особенностями по сравнению с ЦПУ являются: архитектура, максимально нацеленная на увеличение скорости расчёта текстур и сложных графических объектов; ограниченный набор команд.

Примером может служить чип R520 от ATI или G70 от nVidia.

Организация вычислений на графе.

Потоковая архитектура (data-flow) вычислительных систем обеспечивает интерпретацию алгоритмов на графах, управляемых данными. Идеи потоковой обработки информации, организации вычислений, управляемых потоками данных можно рассмотреть на примере организации ввода и суммирования трех чисел. Традиционная схема вычислений может быть представлена так: ввод (а); ввод (в); ввод (с); s = a+в; s = s+c;

Если ввод данных может быть производиться асинхронно, то организовать параллельное программирования данного алгоритма не просто. Параллельный алгоритм может быть записан в виде потока данных на графе: 

 ввод (а)	ввод (в)	ввод (с)
          а+в     а+с       в+с
   (в+с)+а    (а+с)+в          (а+в)+с

Здесь, начальные вершины - ввод, затем каждое введенное данное размножается на три и они передаются на вершины, обеспечивающие суммирование. Теперь, при любом порядке поступления данных отсутствуют задержки вычислений для получения результата. Data-flow программы записываются в терминах графов. В вершинах графа находятся команды, состоящие, например, из оператора, двух операндов (для двуместных операций), возможно, литеральных, или шаблонов для заранее неизвестных данных и ссылки, определяющей команду - наследника и позицию аргумента в ней для результата. Для фрагмента программы, вычисляющего оператор: a=(b+1)*(b-c), команды могут иметь вид: 

L1:(+(<b>) "1" L3/1)
L2:(-(<b>) (<c>) L3/2)
L3:(*( ) ( ) <a>)

Семантика выполнения команд следующая: операция команды Li выполняется, когда поступили все данные для их входных аргументов. Последний параметр у этих команд указывает, кому и куда передавать полученные результаты (в примере это узел, команда L3, а - аргументы 1,2), в терминах графов содержит инструкцию для обмена данных.

Реализация потоковых машин.

Основными компонентами потоковой ВС являются:

  • память команд (ПК),
  • селекторная (арбитражная) сеть,
  • множество исполнительных (функциональных) устройств (ФУ),
  • распределительная сеть. 
                        _______________
       |--------------->|     ФУ      |-----------------|
       |                |_____________|                 |
       |                                                |
селекторная сеть                               распределительная сеть
       |                 ______________                 |
       |<---------------|     ПК       |---------------|
                        |______________|

Память команд состоит из "ячеек" активной памяти, каждая из которых может содержать одну команду вида <метка>: <операция>,<операнд1>,..,<операндК>,<адр_рез1>,..,<адр. _рез.М>, где адреса результатов являются адресами ячеек памяти. С каждой командой связан подсчитывающий элемент, непрерывно ожидающий прибытие аргументов, который пересылает команду на выполнение при наличии полного комплекта аргументов. Активных характер памяти заключается в том, что ячейка, обладающая полным набором операндов, переходит в возбужденное состояние и передает в селекторную сеть информационный пакет, содержащий необходимую числовую и связующую информацию о команде. Селекторная сеть обеспечивает маршрут от каждой командной ячейки к выбранному, в соответствии с кодом операции, исполнительному (функциональному) устройству из множества устройств. Пакет поступает на одно из исполнительных устройств, где соответствующая операция выполняется и результат подается в распределительную сеть. Распределительная сеть обрабатывает результирующий пакет, состоящий из результатов вычислений и адресов назначения. В зависимости от содержимого пакета, результат вычислений поступает в соответствующие ячейки памяти команд, создавая, тем самым, условия возможности их активизации.

Потоковая архитектура (data-flow), как одна из альтернатив фон-Нейманновской, обладает следующими характерными чертами:

  • отсутствие памяти как пассивного устройства, хранящего потребляемую информацию,
  • отсутствие счетчика команд (и, следовательно, последовательной обработки команд программы, разветвлений по условию и т.д.).

Потоковые вычислительные системы позволяют использовать параллелизм вычислительных алгоритмов различных уровней, потенциально достигать производительность, недоступную традиционным вычислительным системам. Основные проблемы, препятствующие развитию потоковых машин:

  1. Не решена проблема создания активной памяти большого объема, допускающей одновременную активизацию большого количества операций.
  2. Создание широкополосных распределительных и селекторных сетей потоковых машин и систем управления коммуникационной сетью является сложной задачей.
  3. Обработка векторных регулярных структур через механизмы потока данных менее эффективна, чем традиционные решения.
  4. Языки программирования для потоковых машин существуют, в основном, в виде графических языков машинного уровня. Языки типа SISAL, ориентируемые на описания потоковых алгоритмов, достаточно сложны для программистов.

Нейронные сети как вычислители.

в Википедии

Измерения производительности ЭВМ.

Обычно, рассматриваются три подхода к оценке производительности:

  • на базе аналитических модели (системами массового обслуживания);
  • имитационное моделирование;
  • измерения.

Первый подход обеспечивает наиболее общие и наименее точные ре¬зультаты, последние, наоборот, - наименее общие и наиболее точные. Измерения проводятся контрольными (тестовыми) программами. Бенч-марк (Benchmark) - эталон:

  • стандарт, по которому могут быть сделаны измерения или сравнения;
  • процедура, задача или тест, которые могут быть использованы для сравнения систем или компонентов друг с другом или со стандартом как в п.1.

Для повышения общности и представительности оценки производительности контрольные программы можно разделить на:

  • программы нижнего уровня. Эти программы тестируют основные машинные операции - +,/,* , с учетом времени доступа к памяти, работу кэша, характеристики ввода/вывода.
  • ядра программ. Ядра программ - короткие характерные участки программ, например, Ливерморские фортрановские ядра (24 ядра) , Эймсовские ядра НАСА, синтетический тест Ветстоун (Whetstone).
  • основные подпрограммы и типовые процедуры; Примером основных подпрограмм могут быть программы Линпак (Linpack) , программы типа быстрого преобразования Фурье. Программа Линпак - процедура решения системы линейных уравнений методом исключения Гаусса. В этой схеме вычислений точно известно число операций с плавающей точкой, которое зависит от размерности массивов – параметров. Стандартные значения размерностей 100 или 1000. Для параллельных ЭВМ имеется соответствующая версия теста.
  • полные основные прикладные программы; В качестве примеров программ этого уровня приводятся Лос-Аламосские тестовые программы моделирования поведения плазмы и программы гидродинамики.
  • перспективные прикладные программы.

Реальная и полная производительность вычислителей.

Оценка производительности вычислительных систем имеет два аспекта: оценка пиковой производительности – номинального быстродействия системы и получение оценок максимальной - “реальной” производительности. Если номинальная(пиковая, предельная) оценка однозначно определяется техническими параметрами оборудования, то вторая характеристика указывает производительность системы в реальной среде применения. Для оценки производительности вычислительных систем в ТОР500 используются обозначения Rpeak – пиковая, предельная производительность и Rmax – максимальная производительность при решении задачи Linpack. Наиболее абстрактной единицей измерения производительности микропроцессоров является тактовая частота ПК, частота тактового генератора (clock rate,). Любая операция в процессоре не может быть выполнена быстрее, чем за один такт (период) генератора. Итак, минимальное время исполнения одной логической операции (переключение транзистора) - один такт. Тактовая частота измеряется в Герцах – число тактов в секунду. Другой обобщенной мерой производительности ПК может служить число команд, выполняемые в единицу времени. Для вычислителей фон-Нейманновской архитектуры скорость выполнения команд уже может быть параметром, который может быть использован для оценки времени выполнения программы. Этот параметр - MIPS (Million Instruction Per Second)- миллион операций (команд, инструкций ЭВМ)/сек. Так как время выполнения различных команд может различаться, то данных параметр сопровождался разного вида уточнениями (логических команд, заданной смеси команд и т.д.), а также наиболее известной здесь мерой в 1 MIPS – это производительность вычислителя VAX 11/780. Итак, данный параметр также достаточно условен. Так как для большинства вычислительных алгоритмов существуют оценки числа арифметических операций, необходимых для выполнения расчетов, данная мера и может служить тем показателем, который и интересует пользователей в первую очередь. Это – MFLPOPS (Million of Floating point Operation Per Second – Мегафлопс)- миллион операций на данных с плавающей запятой/сек, единица быстродействия ЭВМ в операциях с плавающей запятой, есть также единицы - GFLPOPS и ТFLPOPS (терафлопс = 10**12 оп./сек.).

Пакеты для измерения производительности вычислительных систем.

LINPACK

Linpack — программная библиотека, написанная на языке Фортран, которая содержит набор подпрограмм для решения систем линейных алгебраических уравнений.

Linpack была разработана для работы на суперкомпьютерах, которые использовались в 1970-х — начале 1980-х годов.

В настоящее время Linpack заменена другой библиотекой — Lapack, которая работает более эффективно на современных компьютерах.

Существуют версии библиотеки для чисел с плавающей запятой с разной точностью и для комплексных чисел. Появилась реализация библиотеки, написанная на Си. Однако последние версии программы Linpack на языке Си не дают оснований для уверенности в адекватности выдаваемых результатов.

SPEC-89

оффсайт

Standard Performance Evaluation Corporation -- non-profit, industry-sponsored organization

Three main SPEC versions

  • SPEC89
  • SPECint92/SPECfp92
  • SPEC95 Base/Peak int/fp
  • SPEC CPU 2000

SPEC 89:

  • Integer and floating point combined
  • Normalized to a VAX-11/780 (VUP)
  • Geometric mean of individual relative times
  • Ad-hoc collection, many programs small enough to be cached

Параметры рейтинга ТОР500.

TOP 500

  • Номер в списке
  • Производитель
  • Computer - Type indicated by manufacturer or vendor
  • Installation Site - Customer
  • Страна
  • Год последнего обновления информации о системе
  • Field of Application
  • Количество процессоров
  • Rmax - максиальная производительность, достигнутая на тесте LINPACK
  • Rpeak - теоретическая пиковая производительность
  • Nmax - Problem size for achieving Rmax
  • N1/2 - Problem size for achieving half of Rmax

Закон Амдала.

Закон Амдала показывает коэффициент ускорения выполнения программы на параллельных системах в зависимости от степени распараллеливания программы. Пусть: N - число процессоров системы, P - доля распараллеливаемой части программы, а S = 1-P - доля скалярных операций программы, выполняемых без совмещения по времени.( S+P = 1 , S,P >= 0). Тогда, по Амдалу, общее время выполнения программы на однопроцессорном вычислителе S+P, на мультипроцессоре: S+P/N, а ускорение при этом есть функция от P: Sp = (S+P)/(S+P/N) = 1/(S+P/N).

Из формулы закона Амдала следует,что при:

P = 0 S = 1 - ускорения вычисления нет, а

P = 1 S = 0 - ускорение вычислений в N раз

Если P = S = 0.5, то даже при бесконечном числе процессоров уско­рение не может быть более чем в 2 раза.

Параллельные алгоритмы. Метрики.

DOP (Degree Of Parallelism)

Степень параллелизма программы – D(t) – число процессоров, участвующих в исполнении программы в момент времени t. DOP зависит от алгоритма программы, эффективности компиляции и доступных ресурсов при исполнении. График D(t) – профиль параллелизма программы.

Speedup

  • T(n) – время исполнения программы на n процессорах
  • T(n)<T(1), если параллельная версия алгоритма эффективна
  • T(n)>T(1), если накладные расходы (издержки) реализации параллельной версии алгоритма чрезмерно велики

Ускорение за счёт параллельного выполнения S(n) = T(1) / T(n)

Efficiency

Эффективность системы из n процессоров E(n) = S(n) / n

  • Случай S(n)=n – линейное ускорение – масштабируемость (Scalability) алгоритма (возможность ускорения вычислений пропорционально числу процессоров)
  • Случай S(n)>n – суперлинейное ускорение (например, из-за большего коэффициента кеш-попаданий)

Параллельные алгоритмы редукции.

Пусть группа вычислений может производиться параллельно, использую результаты вычислений, выполненных на предыдущих этапах (полученных в виде начальных данных). Тогда, каж¬дая группа вычислений называется "ярусом" параллельной формы, число групп - "высотой", максимальное число операций в группе "шириной" параллельной формы. Один и тот же алгоритм может иметь несколько представлений в виде параллельных форм, различающиеся как шириной, так и высотой. Редукционный алгоритм сдваивания для суммирования чисел с получением частных сумм может иметь вид: 

Данные	  А1   А2    А3   А4    А5   А6     А7   А8
Ярус 1	   А1+А2     А3+А4      А5+А6	     А7+А8
Ярус 2    А12+А3    А12+А34    А56+А7	    А56+А78
Ярус 3   А1234+А5  А1234+А56  А1234+А567  А1234+А5678

Высота параллельной формы равна трем, ширина - четырем, причем загрузка вычислителей (четырех) полная. В данном алгоритме производится вычисления пяти "лишних" чисел по сравнению с последовательным алгоритмом сложения восьми чисел.

Распараллеливание алгоритмов рекурсии первого порядка.

При рекурсивных операциях значение каждого очередного члена последовательности или элемента структуры зависит от значений одного или нескольких предшествующих членов. На ИГ (информационном графе) рекурсия отражается последовательностью одинаковых подграфов, так что результаты предшествующего подграфа являются исходными данными для последующего. В последовательных ЭВМ рекурсия реализуется в виде циклических процессов. Рекурсия встречается не только при числовой обработке, но и при обработке сигналов, операциями над символами и т.п. Рекурсивный характер обработки накладывает ограничения на возможности распараллеливания, которое может быть достигнуто лишь реорганизацией последовательности обработки.

Остановимся на простейшем примере линейной рекурсии первого порядка для вычисления суммы 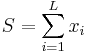S=\sum_{i=1}^L x_i всех элементов вектора 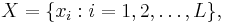X = \{x_i : i = 1, 2,\dots, L\}, для нахождения этой суммы можно воспользоваться рекурсивным соотношением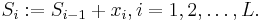 S_i:= S_{i-1} + x_i, i = 1, 2, \dots , L.

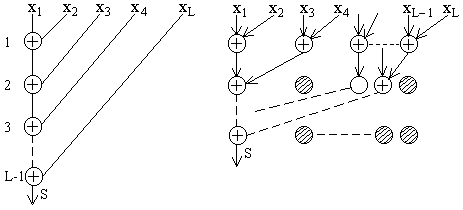
Изображение:Rec_scheme_fig1.gif

Информационный граф на Рис.1а иллюстрирует рекурсивный способ вычисления суммы, и поскольку каждый из операндов используется однократно, такой граф представляет собой бинарное дерево. Если выполнение каждой примитивной операции занимает интервал t, то суммарные затраты времени (и длина графа q) при реализации этого ИГ составят T = (L − 1) * t;q = (L − 1).

При наличии нескольких вычислителей очевидно, что такой алгоритм будет неэффективным, и задача состоит в том, чтобы минимизировать высоту дерева. Преобразование выполняется в соответствии с законами коммутативности, ассоциативности и дистрибутивности, в результате чего может быть получен трансформированный ИГ, показанный на Рис.1б.

Высота такого дерева q' = log2L, а длительность реализации составит T' = t * log2L в предположении, что операции реализуются за то же время t и что затраты времени на обмен между отдельными вычислителями эквивалентны затратам времени на обмен между ячейкой памяти и вычислителем в последовательной структуре. Такой метод нахождения суммы элементов вектора получил название метода сдваивания или метода нахождения параллельных каскадных сумм.

Максимальное ускорение T / T' можно оценить как O(L / log2L), оно достигается при числе вычислителей не менее N = L / 2, причем полностью все L / 2 вычислители загружены только на первом шаге вычислений, на последнем шаге используется лишь один вычислитель.

Не используемые на каждом шаге вычислители можно отразить на ИГ в виде "пустых" операторов, которые показаны на Рис.1б в виде заштрихованных кружочков. Эти пустые операторы не имеют входных и выходных дуг. Теперь можно оценить эффективность полученного алгоритма как отношение числа действительных к общему действительных и пустых операторов. Очевидно, что понятие эффективности сродни понятию коэффициента полезного действия.

Для рассматриваемого алгоритма эффективность составляет 1/2 и не зависит от L.

Векторизация последовательных программ.

Под векторизацией понимается распараллеливание. Наибольшим внутренним параллелизмом, который можно использовать для векторизации программ, являются циклические участки, так как на них приходится основное время вычислений, и в случае распараллеливания вычисления в каждой ветви производится по одному и тому же алгоритму. В методах распараллеливания циклов используется довольно сложный математический аппарат. Наиболее распространенными методами распараллеливания являются: метод параллелепипедов, метод координат, метод гиперплоскостей. Объектами векторизации в этих методах являются циклы типа DО в Фортране.

Метод координат

Обеспечивает векторизацию циклов для синхронных ЭВМ (ОКМД - SIMD архитектуры). Семантика синхронных циклов следующая:

  • для каждой итерации цикла назначается процессор;
  • вычисления должны производиться всеми процессорами (процессорными элементами) параллельно и синхронно.

Операторы тела цикла выполняются по очереди, но каждый оператор выполняется всеми процессорами одновременно. При выполнении оператора присваивания сначала вычисляется правая часть, затем одновременно выполняется операция присваивания для всех элементов массива левой части.

Теоретическое обоснование классического метода координат предложено Лэмпортом. Метод применим для канонических ("чистых") циклов, тела которых состоят только из операторов присваивания, причем управляющая переменная заголовка цикла (параметр цикла) должна входить в индексные выражения операторов тела цикла линейно. Метод предназначен для синхронной векторизации одномерных циклов (многомерные циклы можно рассматривать по каждому параметру отдельно). Идея данного метода состоит в том, что для индексов, содержащих параметры цикла, рассматривается порядок следования, который и определяет очередность выборки/записи соответствующего элемента массива. Так как рассматриваются только линейные индексные выражения, порядок следования определяется значениями соответствующих алгебраических выражений. Строится граф характеристических множеств всех индексов, и при отсутствии в графе петель делается заключение о возможности векторизации всего цикла.

В некоторых случаях (устранимая векторная зависимость) векторизация возможна лишь в случае переупорядочивания - перестановки операторов цикла или путем введения временной переменной (массива), куда будут копироваться элементы вектора для защиты перед их изменением для последующего использования в исходном виде. Итак, метод координат:

  • позволяет определить возможность выполнения цикла в синхронном режиме;
  • содержит алгоритмы преобразования тела цикла к синхронному виду.

Например, по Лэмпорту, цикл: {{{ 

      DO 24 I=2,M
      DO 24 J=2,N
21    A(I,J) = B(I,J)+C(I)
22    C(I) = B(I-1,J)
23    B(I,J) = A(I+1,J) ** 2
24    CONTINUE

}}} преобразуется в цикл: {{{ 

      DO 24 J=2,N
      DO 24  SIM FOR ALL I {i:2<=i<=M}
      /* SIM - SIMulteneusly (одновременно)*/ 
      TEMP(I) = A(I+1,J)
21    A(I,J) = B(I,J)+C(I)
23    B(I,J) = TEMP(I) ** 2
22    C(I) = B(I-1,J)
24    CONTINUE

}}}

Примеры векторизации

Исходные и преобразованные тела циклов: 

A(I) = B(I)                 C(I) = A(I+1)
C(I) = A(I+1)               A(I) = B(I)

A(I) = B(I)                 D(I) = A(I)
C(I) = A(I) + A(I+1)        A(I) = B(I)
                            C(I) = A(I) + D(I+1)

A(I) = B(I) + B(I+1)        D(I) = B(I)
B(I) =  A(I+1)              B(I) = A(I+1)
                            A(I) = D(I) + B(I+1)

A(I) = B(I) + B(I-1)          Векторизация невозможна
B(I) =  A(I)

Метод гиперплоскостей

Метод гиперплоскостей применим только к многомерным циклам. В пространстве итераций ищется прямая (плоскость), на которой возможно параллельное асинхронное выполнение тела цикла, причем в отличие от метода координат, эта прямая (плоскость) может иметь наклон по отношению к осям координат. Цикл вида: 

   DO 5  I = 2,N
   DO 5  J = 2,M
5  A(I,J) = ( A(I-1,J) + A(I,J-1) ) * 0.5

Методом координат не векторизуется. Действительно, при фиксированном значении переменной I (I = i) значение, вычисленное в точке (i,j) пространства итераций, зависит от результата вычислений в предыдущей точке (i,j-1) , так что параллельное выполнение тела цикла по переменной J невозможно. Аналогично нельзя проводить параллельные вычисления по переменной I. Метод гиперплоскостей применим только к многомерным циклам. В пространстве итераций ищется прямая (плоскость), на которой возможно параллельное асинхронное выполнение тела цикла, причем в отличие от метода координат, эта прямая (плоскость) может иметь наклон по отношению к осям координат. Цикл вида: 

   DO 5  I = 2,N
   DO 5  J = 2,M
5  A(I,J) = ( A(I-1,J) + A(I,J-1) ) * 0.5

Методом координат не векторизуется. Действительно, при фиксированном значении переменной I (I = i) значение, вычисленное в точке (i,j) пространства итераций, зависит от результата вычислений в предыдущей точке (i,j-1) , так что параллельное выполнение тела цикла по переменной J невозможно. Аналогично нельзя проводить параллельные вычисления по переменной I.

Однако можно заметить, что результат будет также правильным, если вычисления проводить в следующем порядке:

  • на 1-м шаге - в точке (2,2),
  • на 2-м шаге - в точках (3,2) и (2,3),
  • на 3-м шаге - в точках (4,2), (3,3) и (2,4),
  • на 4-м шаге - в точках (5,2), (4,3), (3,4) и (2,5)

Вычисления в указанных точках для каждого шага, начиная со второго, можно проводить параллельно и асинхронно. Перечисленные кортежи точек лежат на параллельных прямых вида I+J=K , а именно: на первом шаге - на прямой I+J=4 , на втором - I+J=5, на третьем шаге - I+J=6 и т.д., на последнем ((N-2)+(M-2)+1) - ом шаге - на прямой I+J=M+N.

В общем случае для n-мерного тесногнездового цикла ищется семейство параллельных гиперплоскостей в n-мерном пространстве итераций, таких что во всех точках каждой из этих гиперплоскостей возможно параллельное выполнение тела цикла.

Для приведенного примера множество точек, в которых возможно параллельное выполнение, является однопараметрическим (прямая) и определяется из решения уравнения 1I+J=K 0. Цикл (5) может быть преобразован к виду: 

DO 5   K = 4,M+N
Tн = MMAX(2,K-N)
Tк = MMIN(M,K-2)
DO 5  T = Tн,Tк  1: PAR
I  = T
J  = K - T
5  A(I,J) = ( A(I-1,J) + A(I,J-1) ) * 0.5

Функция MMAX(X,Y) выбирает ближайшее целое, большее или равное максимуму из чисел X и Y , а функция MMIN(X,Y) - ближайшее целое, меньшее или равное минимуму из X и Y .

Внутренний цикл по переменной T может выполняться параллельно для всех значений T . Границы изменения переменной цикла T меняются при переходе с одной прямой (гиперплоскости) на другую, поэтому их необходимо перевычислять во внешнем цикле. Число итераций внутреннего цикла, то есть потенциальная длина векторной операции, меняется с изменением K . Для приведенного примера диапазон изменения T сначала возрастает, а потом убывает, причем для начального и конечного значения K он равен единице. В некоторых случаях для отдельных значений K накладные расходы на организацию векторного вычисления могут превысить эффект ускорения от векторного выполнения.

Метод параллелепипедов

Идея метода заключается в выявлении зависимых итераций цикла и объединении их в последовательности - ветви, которые могут быть выполнены независимо друг от друга. При этом в пространстве итераций определяются области (параллелепипеды), все точки которых принадлежат разным ветвям. Задача максимального распараллеливания заключается в поиске параллелепипеда наибольшего объема; тогда исходный цикл выполняется наибольшим числом параллельных ветвей, каждая из которых представляет собой исходный цикл, но с другим шагом изменения индекса. Для исходного цикла: 

  DO 7  I = 1,7
  DO 7  J = 1,3

7 X(I,J) = X(I-2,J-1) параллельное представление в виде: 

 DO 7  (K,L) = (1,1) (P1,P2)   1:  PAR
 DO 7  I = K,7,P1
 DO 7  J = L,3,P2

7 X(I,J) = X(I-2,J-1) допускается для различных разбиений пространства итераций: пара (P1,P2) может иметь, например, значения (2,1), (2,3) или (7,1). Таким образом, исходный цикл (7) преобразуется в последовательность параллельных ветвей, имеющих циклический вид.

В общем виде задача, рассматриваемая методом параллелепипедов, для одномерных циклов состоит в определении возможности представления цикла: 

DO L  I = 1,r
L  T(I)

(где T(i) - тело цикла) в виде следующей языковой конструкции: 

DO L  K = 1,p   1: PAR
DO L  I = K,r,p
L  T(I)

Оценка возможности векторизации

Оценить возможность параллельного выполнения цикла: 

 DO i = 2,N
   A(i) = (B(i) + C(i))/A(i+CONST)
  ENDDO

Если const = 0, то все итерации цикла независимы и такой цикл может быть выполнен на любой многопроцессорной ЭВМ, влючая Иллиак-4. (каждый виток цикла выполняется на отдельном процессоре). Если const > 0 (пусть =1) то при параллельное выполнение цикла на ЭВМ класса МКМД без дополнительных мер по синхронизации работы процессоров невозможно. Например, пусть N=3 и два процессора вычисляют параллельно эти итерации, тогда, первый процессор вычисляет А2 по В2, С2, А3, а второй, А3 по В2, С2, А4 . При отсутствии синхронизации может случиться ситуация, при которой второй процессор завершит свою работу до начала работы первого. Тогда первый процессор для вычислений будет использовать А3, которое обновил второй процессор, что неверно, ибо здесь нужно “старое” значение А3. Однако, этот цикл выполняется параллельно на ЭВМ ОКМД (SIMD) так как там этот цикл может быть выполнен такими командами:

  • Считать Вi в сумматоры каждого из n АЛУ.
  • Сложить Сi со своим содержимом сумматора.
  • Разделить содержимое каждого i-сумматора на Аi+1.
  • Записать содержимое i- сумматоров в Аi.

Из за того, что выборка из памяти и запись в память производится синхронно (одновременно), то работа цикла – корректна. Если const < 0 то параллельное выполнение цикла невозможно, ибо для выполнения очередной итерации цикла необходимы результаты работы предыдущей (рекурсия). Однако известны приемы преобразования такого рода циклов к виду, допускающие параллельное выполнение.

Синхронизация параллельных процессов.

[2]

Параллельная программа - это множество параллельных процессов, синхронизирующих свою работу и обменивающихся данными посредством передачи сообщений.

Основным механизмом синхронизации параллельных процессов, взаимодействующих с помощью передачи сообщений, является барьер. Барьер - это точка параллельной программы, в которой процесс ждёт все остальные процессы, с которыми он синхронизирует свою работу. Лишь только после того, как все процессы, синхронизирующие свою работу, достигли барьера, они продолжают дальнейшие вычисления. Если по какой-то причине хотя бы один из этих процессов не достигает барьера, то остальные процессы "зависают" в этой точке программы, а программа в целом уже никогда не сможет завершиться нормально.

Исполняемые комментарии в языках программирования.

Система Open MP.

OpenMP (Open Multi-Processing) это набор директив компилятора, библиотечных процедур и переменных окружения, которые предназначены для программирования многопоточных приложений на многопроцессорных системах с единой памятью на языках C, C++ и Fortran.

Разработку спецификации OpenMP ведут несколько крупных производителей вычислительной техники и программного обеспечения, чья работа регулируется некоммерческой организацией, называемой OpenMP Architecture Review Board (ARB).

OpenMP реализует параллельные вычисления с помощью многопоточности, в которой «главный» (master) поток создает набор подчиненных (slave) потоков и задача распределяется между ними. Предполагается, что потоки выполняются параллельно на машине с несколькими процессорами (количество процессоров не обязательно должно быть больше или равно количеству потоков).

Задачи, выполняемые потоками параллельно, также как и данные, требуемые для выполнения этих задач, описываются с помощью специальных директив препроцессора соответствующего языка — прагм. Например, участок кода на языке Fortran, который должен исполняться несколькими потоками, каждый из которых имеет свою копию переменной N, предваряется следующей директивой: !$OMP PARALLEL PRIVATE(N)

Количество создаваемых потоков может регулироваться как самой программой при помощи вызова библиотечных процедур, так и извне, при помощи переменных окружения.

Ключевыми элементами OpenMP являются 

   * конструкции для создания потоков (директива parallel),
   * конструкции распределения работы между потоками (директивы DO/for и section),
   * конструкции для управления работой с данными (выражения shared и private),
   * конструкции для синхронизации потоков (директивы critical, atomic и barrier),
   * процедуры библиотеки поддержки времени выполнения (например, omp_get_thread_num),
   * переменные окружения (например, OMP_NUM_THREADS).


Ниже приведены примеры программ с использованием директив OpenMP: Fortran 77

В этой программе на языке Fortran создается заранее неизвестное число потоков (оно определяется переменной окружения OMP_NUM_THREADS перед запуском программы), каждый из которых выводит приветствие вместе со своим номером. Главный поток (имеющий номер 0) также выводит общее число потоков, но только после того, как все они «пройдут» директиву BARRIER. 

     PROGRAM HELLO
     INTEGER ID, NTHRDS
     INTEGER OMP_GET_THREAD_NUM, OMP_GET_NUM_THREADS
     
     C$OMP PARALLEL PRIVATE(ID)
     
     ID = OMP_GET_THREAD_NUM()
     PRINT *, 'HELLO WORLD FROM THREAD', ID
     
     C$OMP BARRIER
     
     IF ( ID .EQ. 0 ) THEN
       NTHRDS = OMP_GET_NUM_THREADS()
       PRINT *, 'THERE ARE', NTHRDS, 'THREADS'
     END IF
     
     C$OMP END PARALLEL
     
     END


В этой программе на языке С два вектора (a и b) складываются параллельно десятью потоками. 

 #include <stdio.h>
 #include <omp.h>
 #define N 100
 int main(int argc, char *argv[])
 {
 float a[N], b[N], c[N];
 int i;
 omp_set_dynamic(0);      // запретить библиотеке openmp менять число потоков во время исполнения
 omp_set_num_threads(10); // установить число потоков в 10

 // инициализируем векторы
 for (i = 0; i < N; i++)
 {
     a[i] = i * 1.0;
     b[i] = i * 2.0;
 }

 // вычисляем сумму векторов
 #pragma omp parallel shared(a, b, c) private(i)
 {
 #pragma omp for
   for (i = 0; i < N; i++)
     c[i] = a[i] + b[i];
 }
 printf ("%f\n", c[10]);
 return 0;
 }

OpenMP поддерживается многими коммерческими компиляторами.

  1. Компиляторы Sun Studio поддерживают официальную спецификацию — OpenMP 2.5 [2] - с улучшенной производительностью под ОС Solaris; поддержка Linux запланирована на следующий релиз.
  2. Visual C++ 2005 поддерживает OpenMP в редакциях Professional и Team System [3].
  3. GCC 4.2 поддерживает OpenMP, а некоторые дистрибутивы (такие как Fedora Core 5 gcc) включили поддержку в свои версии GCC 4.1.
  4. Intel C Compiler
  5. IBM XL compiler
  6. PGI (Portland group)
  7. Pathscale
  8. HP

Пакет MPI.

Язык Фортран-GNS.

http://www.keldysh.ru/papers/2006/prep08/prep2006_08.html

Порождение параллельных процессов. Идентификация абонентов.

Протоколы передачи сообщений.

Учет топологии кластера в МР программировании.

Язык Фортран-DVM.

DVM-система предоставляет единый комплекс средств для разработки параллельных программ научно-технических расчетов на языках Си и Фортран 77.

Модель параллелизма DVM. Модель параллелизма DVM базируется на модели параллелизма по данным. Аббревиатура DVM отражает два названия модели: распределенная виртуальная память (Distributed Virtual Memory) и распределенная виртуальная машина (Distributed Virtual Mashine). Эти два названия указывают на адаптацию модели DVM как для систем с общей памятью, так и для систем с распределенной памятью. Высокоуровневая модель DVM позволяет не только снизить трудоемкость разработки параллельных программ, но и определяет единую формализованную базу для систем поддержки выполнения, отладки, оценки и прогноза производительности.

Языки и компиляторы. В отличие от стандарта HPF в системе DVM не ставилась задача полной автоматизации распараллеливания вычислений и синхронизации работы с общими данными. С помощью высокоуровневых спецификаций программист полностью управляет эффективностью выполнения параллельной программы. С другой стороны, при проектировании и развитии языка Fortran DVM отслеживалась совместимость с подмножеством стандартов HPF1 и HPF2.

Единая модель параллелизма встроена в языки Си и Фортран 77 на базе конструкций, которые “невидимы” для стандартных компиляторов, что позволяет иметь один экземпляр программы для последовательного и параллельного выполнения. Компиляторы с языков C-DVM и Fortran DVM переводят DVM-программу в программу на соответствующем языке (Си или Фортран 77) с вызовами функций системы поддержки параллельного выполнения. Поэтому единственным требованием к параллельной системе является наличие компиляторов с языков Си и Фортран 77.

Технология выполнения и отладки. Единая модель параллелизма позволяет иметь для двух языков единую систему поддержки выполнения и, как следствие, единую систему отладки, анализа и прогноза производительности. Выполнение и отладка DVM-программ может осуществляться в следующих режимах: Последовательное выполнение и отладка средствами стандартных компиляторов с языков Си и Фортран 77. Псевдо-параллельное выполнение на рабочей станции (среда WINDOWS и UNIX). Параллельное выполнение на параллельной ЭВМ.

При псевдо-параллельном и параллельном выполнении возможны следующие режимы отладки: автоматическая проверка правильности директив параллелизма; трассировка и сравнение результатов параллельного и последовательного выполнения; накопление и визуализация трассировки данных; накопление данных о производительности и прогноз производительности параллельного выполнения.

Язык Fortran DVM (FDVM) представляет собой язык Фортран 77 [5], расширенный спецификациями параллелизма. Эти спецификации оформлены в виде специальных комментариев, которые называются директивами. Директивы FDVM можно условно разделить на три подмножества:

  1. Распределение данных
  2. Распределение вычислений
  3. Спецификация удаленных данных

Модель параллелизма FDVM базируется на специальной форме параллелизма по данным: одна программа – множество потоков данных (ОПМД). В этой модели одна и та же программа выполняется на каждом процессоре, но каждый процессор выполняет свое подмножество операторов в соответствии с распределением данных.

В модели FDVM пользователь вначале определяет многомерный массив виртуальных процессоров, на секции которого будут распределяться данные и вычисления. При этом секция может варьироваться от полного массива процессоров до отдельного процессора.

На следующем этапе определяются массивы, которые должны быть распределены между процессорами (распределенные данные). Эти массивы специфицируются директивами отображения данных. Остальные переменные (распределяемые по умолчанию) отображаются по одному экземпляру на каждый процессор (размноженные данные). Размноженная переменная должна иметь одно и то же значение на каждом процессоре за исключением переменных в параллельных конструкциях.

Модель FDVM определяет два уровня параллелизма: параллелизм по данным на секции массива процессоров; параллелизм задач – независимые вычисления на секциях массива процессоров.

Параллелизм по данным реализуется распределением витков тесно-гнездового цикла между процессорами. При этом каждый виток такого параллельного цикла полностью выполняется на одном процессоре. Операторы вне параллельного цикла выполняются по правилу собственных вычислений.

Параллелизм задач реализуется распределением данных и независимых вычислений на секции массива процессоров.

При вычислении значения собственной переменной процессору могут потребоваться как значения собственных переменных, так и значения несобственных (удаленных) переменных. Все удаленные переменные должны быть указаны в директивах доступа к удаленным данным.

Система программирования НОРМА.

Язык Норма является специализированным языком и предназначен для спецификации численных методов решения задач математической физики. Изначально он был ориентирован на решение задач математической физики разностными методами, однако, как показала практика, может быть использован для решения более широкого класса вычислительных задач.

Первоначально термин Норма расшифровывался следующим образом: Непроцедурное Описание Разностных Моделей Алгоритмов. Сейчас мы считаем уместной и другую трактовку - это Нормальный уровень общения прикладного математика с ЭВМ: расчетные формулы, полученные им в процессе решения прикладной задачи, почти непосредственно используются для ввода в вычислительную систему и проведения счета.

В записи на Норме не требуется никакой информации о порядке счета, способах организации вычислительных (циклических) процессов. Порядок предложений языка может быть произвольным -- информационные взаимосвязи выявляются и учитываются транслятором при организации вычислительного процесса. Программа на языке Норма может рассматриваться как описание запроса на вычисление, а реализация этого запроса с учетом архитектуры ЭВМ и возможностей выходного языка - то есть синтез выходной программы - возлагается на транслятор.

Выбор уровня языка Норма определяет характерную его черту - это язык с однократным присваиванием, то есть каждая переменная может принимать значение только один раз. Такие понятия, как память, побочный эффект, оператор присваивания, управляющие операторы в языке Норма отсутствуют по определению.

Эти свойства, и некоторые другие ограничения (в первую очередь, на вид индексных выражений и способы описания индексных пространств), позволяют строго обосновать разрешимость задачи синтеза выходной программы [2,3], так как в достаточно общей постановке решение этой задачи приводит к значительным математическим трудностям - она может оказаться NP-полной либо вообще неразрешимой. С другой стороны, исследования, связанные с разработкой и применением языка Норма показывают, что имеющиеся ограничения приемлемы с практической точки зрения [5].

Программа на Норме состоит из одного или нескольких разделов. Разделы могут быть трех видов - главный раздел, простой раздел и раздел-функция, вид раздела определяется ключевыми словами MAIN PART, PART, FUNCTION соответственно.

Разделы могут вызывать друг друга по имени и передавать данные при помощи механизма формальных и фактических параметров, или через внешние файлы при помощи описаний INPUT и OUTPUT. Для каждого раздела справедливо правило локализации: имена, описанные в разделе, локализованы в этом разделе; понятие глобальных переменных в языке отсутствует.

Главный раздел обязательно должен присутствовать в программе на Норме и быть единственным; формальных параметров он не имеет. Вызовы главного раздела, а также рекурсивные вызовы разделов запрещены. В заголовке раздела указывается имя раздела и список формальных параметров. Формальные параметры должны быть описаны в теле раздела при помощи declaration-of-scalar-variables, declaration-of-variables-on-domains или declaration-of-external

Параметры-величины, указанные до ключевого слова RESULT в списке формальных параметров, являются исходными данными для вычислений, описываемых в разделе; параметры, перечисленные после - являются результатами вычислений. Один и тот же параметр не может быть одновременно исходным и результатом: это приводит к переприсваиванию значений переменным (повторному присваиванию), что запрещено в Норме. В разделе-функции ключевое слово RESULT не используется: результат вычисления функции связывается с именем и типом функции.

В теле раздела могут быть заданы описания, операторы и итерации (порядок их расположения, вообще говоря, произвольный - возможные ограничения определяются при описании входного языка транслятора).

Система Норма состоит из следующих компонентов:

  1. Декларативный язык Норма
  2. Компилятор с языка Норма
  3. Конфигуратор программ на языке Норма
  4. Отладчик программ на языке Норма
  5. Пользовательский Windows-интерфейс

Особенности машинной арифметики.

В вычислительных машинах применяются две формы представления чисел:

  • естественная форма или форма с фиксированной запятой (точкой);
  • нормализованная форма или форма с плавающей запятой (точкой);

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной. Например, 32,54; 0,0036; –108,2. Эта форма проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях. Если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки и дальнейшие вычисления теряют смысл. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел. С плавающей запятой числа изображаются в виде X = ±M×P±r, где M - мантисса числа (правильная дробь в пределах 0,1 ≤ M < 1), r - порядок числа (целое), P - основание системы счисления. Например, приведенные выше числа с фиксированной запятой можно преобразовать в числа с плавающей запятой так: 0,3254×102, 0,36×10–2, –0,1082×103. Нормализованная форма представления имеет огромный диапазон чисел и является основной в современных ЭВМ.

Каждому двоичному числу можно поставить в соответствие несколько видов кодов. Существуют следующие коды двоичных чисел:

Прямой код. Прямой код двоичного числа (а это либо мантисса, либо порядок) образуется по такому алгоритму:

  1. Определить данное двоичное число - оно либо целое (порядок), либо правильная дробь (мантисса).
  2. Если это дробь. то цифры после запятой можно рассматривать как целое число.
  3. Если это целое и положительное двоичное число, то вместе с добавлением 0 в старший разряд число превращается в код. Для отрицательного двоичного числа перед ним ставится единица.

Обратный код. Обратный код положительного двоичного числа совпадает с прямым кодом, а для отрицательного числа нужно, исключая знаковый разряд, во всех остальных разрядах нули заменить на единицы и наоборот.

Дополнительный код. Дополнительный код положительного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа образуется путём прибавления 1 к обратному коду.

Сложение и вычитание двоичных чисел. Сложение чисел, а также вычитание чисел в обратном или дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел. Это правило распространяется и на знаковые разряды чисел. Различие же обратного и дополнительного кодов связано с тем, что потом делают с единицей переноса из старшего разряда, изображающего знак числа. При сложении чисел в обратном коде эту единицу надо прибавить к младшему разряду результата, а в дополнительном коде единица переноса из старшего разряда игнорируется.

Умножение и деление двоичных чисел в ЭВМ производится в прямом коде, а их знаки используются лишь для определения знака результата. Также как и в математике, умножение и деление сводится к операциям сдвигов и сложений (с учётом знака числа).

Погрешности параллельных вычислений. Оценить ошибки суммирования.

Источники погрешности при вычислениях на параллельных системах. В общем случае, арифметические операции над элементами дискретного подмножества вещественных чисел F не корректны. Результат арифметических операций чисел с плавающей запятой может:

  • иметь абсолютное значение, больше M (максимального числа) - машинное переполнение;
  • иметь ненулевое значение, меньшее m (минимального числа) по абсолютной величине - машинный нуль;
  • иметь значение в диапазоне [m:M] и тем не не менее не принадлежать множеству F (произведение двух чисел из F, как правило, записывается посредством 2t либо 2t-1 значащих цифр);

Поэтому, на множестве чисел с плавающей запятой определяются и "плавающие" арифметические операции, за результаты которых, если они не выходит за границы множества F, принимается ближайшие по значению элементы F. Примеры из четырехразрядной десятичной арифметики по Н. Вирту.

  1. Пусть x=9.900 y=1.000 z=-0.999 и тогда:
    • (x+y)+z = 9.910
    • x+(y+z) = 9.901
  1. Пусть x=1100. y=-5.000 z=5.001 и тогда:
    • (x*y)+(x*z) = 1.000
    • x*(y+z) = 1.100

Здесь операции + и * - плавающие машинные операции. Такие 'чиcленные' процессы называют иногда 'неточными', здесь нарушаются ассоциативный и дистрибутивный законы арифметики..

Причины возникновения ошибок

Вначале рассмотрим простейший метод вычисления суммы чисел с плавающей точкой.

/* Simple Summation */

float f_add(float * flt_arr)
{
  long i;
  float sum = 0.0;
  for (i = 0; i < ARR_SIZE; i++)
    sum += flt_arr[i];
  return sum;
}

Чаще всего результат применения данного метода оказывается неудовлетворительным. Проблема заключается в том, что складывание чисел с плавающей точкой сильно отличается от применения той же операции к целым числам. И основное отличие между ними — то, что при сложение вещественных чисел сначала их нужно преобразовать так, чтобы складывались цифры чисел одинакового порядка. При этом, если порядки чисел значительно различаются, тогда цифры младших разрядов отбрасываются. Если необходимо найти сумму сравнительно небольшого количества чисел, например, двух или трех, то данную ошибку можно и не заметить. Но при сложении большого множества чисел существенно отличающихся по величине, ошибка вычисления может оказаться неприемлемой.

Приведем простейший пример

Числа в компьютере представляются приближенно, что обусловлено конечностью разрядной сетки . Допустим, что порядок мантиссы не позволяет различить цифры порядка в 10 биллионов. Мы хотим сложить числа: 

1.0 + 1.0e10 + −1.0e10

Выполняя суммирования чисел в различном порядке, мы получаем различный результат: 

(1.0 + 1.0e10) + −1.0e10
  = 1.0e10 + -1.0e10
  = 0.0

но 

1.0 + (1.0e10 + −1.0e10)
  = 1.0 + 0.0
  = 1.0

В первом случае информация о первом слагаемом была полностью потеряна, поскольку два других слагаемых значительно больше по величине. При суммировании небольшого числа слагаемых ошибку можно и не заметить, но при суммировании большого множества чисел с плавающей точкой ошибка будет накапливаться за счет этих небольших погрешностей, и также за счет разницы между промежуточной суммой и текущем членом.

Упорядоченное суммирование

Как было показано выше, ошибка вычисления сильно зависит от порядка выполнения операций. При сложении двух чисел, значительно различающихся по величине, точность вычисления сильно снижается. Представим, что мы суммируем большое множество чисел. Тогда одним из операндов всегда будет сумма, причем в большинстве случаев она по величине значительно превосходит числа, которые мы постепенно к ней прибавляем. Данный эффект потери точности вычислений можно минимизировать путем упорядоченного суммирования чисел от наименьшего к наибольшему по абсолютному значению. 

/* Sorted Summation */

float fs_add(float * flt_arr)
{
  long i;
  float lcl_arr[ARR_SIZE], sum = 0.0;

  for (i = 0; i < ARR_SIZE; i++)
    lcl_arr[i] = flt_arr[i];
  qsort(lcl_arr, ARR_SIZE, sizeof(float),
        flt_abs_compare);
  for (i = 0; i < ARR_SIZE; i++)
    sum += lcl_arr[i];

  return sum;
}

Сначала создаем локальную копию массива flt_arr — lcl_arr. Сортируем полученный массив с помощью qsort. Затем суммируем элементы отсортированного массива. Но результаты по-прежнему остаются неудовлетворительными. Это происходит из-за того, что сумма очень быстро становится значительно больше по порядку, чем прибавляемые числа. В результате этого, точность вычисления повышается незначительно.


На самом деле, особенности суммируемых чисел сильно влияют на сортировку. Лучший случай, когда сумма принимает значения около нуля, а распределение примерно симметричное. Это условие способствует тому, что сумма всегда имеет примерно тот же порядок, что и суммируемые числа. Этот случай рассмотрен на примерах. Однако на практике он встречается довольно редко. Иногда сортировку чисел невозможно предугадать. Упорядоченное суммирование всегда дает один и тот же результат на одних и тех же множеств чисел, даже если числа следуют в разном порядке. Но это не совсем верно в случае, например, если использовать функцию сравнения: 

/* Simple comparison */

int flt_abs_compare(const void * a, const void * b)
{
  float fa = fabs(*(float *)a);
  float fb = fabs(*(float *)b);
  if (fa == fb)
    return 0;
  else if (fa < fb)
    return -1;
  else
    return 1;
}

В этом случае число и обратная (по знаку) ему величина считаются одинаковыми. А это означает, что они могут оказаться в любом порядке следования в упорядоченной последовательности. Когда же нам нужна уверенность, необходимо использовать функцию сравнения вида: 

/* Tie-breaking comparison */

int flt_abs_compare(const void * a,
                    const void * b)
{
  float va = *(float *)a;
  float vb = *(float *)b;
  float fa = fabs(va);
  float fb = fabs(vb);
  if (fa < fb)
    return -1;
  else if (fa > fb)
    return 1;
  else if (va < vb)
    return -1;
  else if (va > vb)
    return 1;
  else
    return 0;
}

Данная функция добивается полной предсказуемости следования элементов.


Оценка полной ошибки для суммирования положительных чисел.

Пример расчета полной ошибки для суммирования положительных чисел Формула полной ошибки для суммирования положительных чисел 

Ai (i=1,..,n) имеет вид: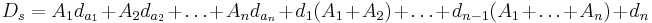   D_s = A_1d_{a_1} + A_2d_{a_2} +\dots+ A_nd_{a_n} + d_1(A_1+A_2) +\dots+ d_{n-1}(A_1+\dots+A_n) + d_n

, где

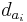d_{a_i} - относительные ошибки представления чисел в ЭВМ, а di - относительные ошибки округления чисел при каждой следующей операции сложения. Пусть: все 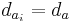d_{a_i} = d_a и di = d, a 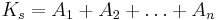K_s = A_1+A_2+\dots+A_n, тогда: D_s = d_aK_s + d[(n-1)A_1+(n-1)A_2 + (n-2)A_3 + \dots+ 2A_{n-1} + A_n]

Очевидно, что наибольший "вклад" в сумму ошибок вносят числа, суммируемые вначале. Следовательно, если суммируемые положительные числа упорядочить по возрастанию, максимально возможная ошибка суммы будет минимальной. Изменяя порядок суммирования чисел можно получать различные результаты. Но если даже слагаемые отличаются друг от друга незначительно, на точность результата может оказать влияние способ суммирования.
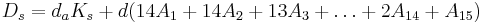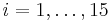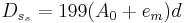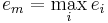Пусть суммируются 15 положительных чисел, тогда ошибка результата: D_s = d_aK_s + d(14A_1+14A_2+13A_3+\dots+2A_{14}+A_{15}). Слагаемое daKs не зависит от способа суммирования, и далее не учитывается. Пусть слагаемые имеют вид: Ai = A0 + ei, где i=1,\dots,15, тогда: D_{s_s} = 199(A_0+e_m)d, где e_m = \max\limits_{i}{e_i}, d - ошибка округления при выполнении арифметической операции сложения. Если провести суммирование этих чисел по группам (три группы по четыре числа и одна группа из трех чисел), то ошибки частных сумм имеют вид:
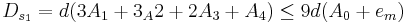
D_{s_1} = d(3A_1+3_A2+2A_3+A_4) \leq 9d(A_0+e_m)
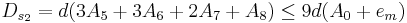
D_{s_2} = d(3A_5+3A_6+2A_7+A_8) \leq 9d(A_0+e_m)
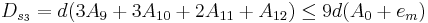
D_{s_3} = d(3A_9+3A_{10}+2A_{11}+A_{12}) \leq 9d(A_0+e_m)
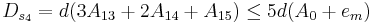
D_{s_4} = d(3A_{13}+2A_{14}+A_{15}) \leq 5d(A_0+e_m)
Полная оценка ошибок округления будет 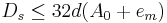D_s \leq 32d(A_0+e_m), что меньше 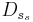D_{s_s}. Итак суммирование по группам дает меньшую ошибку результата. Например, разделив процесс суммирования массива положительных чисел на параллельные процессы, и затем получив сумму частных сумм, можно получить результат, отличный от последовательного суммирования в одном процесс.

Алгоритмы оптимизации программ, влияющие на точность вычислений.

Оптимизационные преобразования программ для их оптимального выполнения на конвейерных вычислителях могут проводиться системами программирования. Эти преобразования, алгебраически эквивалентные, могут нарушить порядок вычислений, предписанный исходным текстом программы. Последствия таких преобразований обсуждались выше. Наиболее характерные преобразования следующие. 

           1. Балансировка  дерева  вычислений

Балансировка дерева вычислений (tree-height reduction or balancing) выражений позволяют использовать конвейерное АУ без пропуска рабочих тактов. Так, вычисление суммы вещественных чисел: A+B+C+D+E+F+G+H, будет запрограммировано как последовательность операций: (((A+B)+(C+D))+((E+F)+(G+H))); это нарушает заданную по умолчанию последовательность вычислений с накоплением одной частной суммы и может повлиять на результат. 

        2. Исключение общих подвыражений

Алгоритмы исключения общих подвыражений (Common subexpession elimination) также могут изменить порядок вычислений. Если компилятор распознает в выражениях повторяющееся вычисление, то это вычисление производятся один раз, его результат сохраняется на регистре, и в дальнейшем используется этот регистр. Тем самым исключается избыточность вычислений. 

    X = A + B + C + D     ---->       REG = B + C
    Y = B + E + C                     X   = A + D + REG
                                    Y   = E + REG

        3. Разворачивание циклов

Разворачивание циклов (loop unrolling) - расписывание цикла последовательностью операторов присваивания: либо полностью, либо размножение тела цикла с некоторым коэффициентом (фактором) размножения. Производится частичное или полное разворачивание цикла в последовательный участок кода. При частичном разворачивании используется так называемый фактор разворачивания (который можно задавать в директиве компилятору). 

    DO I=1,100                  DO I=1,100,4
      A(I) = B(I) + C(I)          A(I) = B(I) + C(I)
    ENDDO                         A(I+1) = B(I+1) + C(I+1)
                                  A(I+2) = B(I+2) + C(I+2)
                                  A(I+3) = B(I+3) + C(I+3)
                                ENDDO

При этом преобразовании снижается количество анализов итерационной переменной. Данный алгоритм также может привести к нарушению предписанного первоначально порядка вычислений. Например: 

    DO I=1,10        DO I=1,10,2
    S = S + A(I)       S = S + A(I)
    ENDDO             S1 = S1 + A(A+1)
                     ENDDO
                     S = S + S1

Здесь, суммирование проводится отдельно для четных и нечетных элементов с последующем сложением частных сумм.

Получено с http://esyr.me/wiki/%D0%9F%D0%9E%D0%94:_%D0%9E%D1%82%D0%B2%D0%B5%D1%82%D1%8B2
Личные инструменты
Разделы