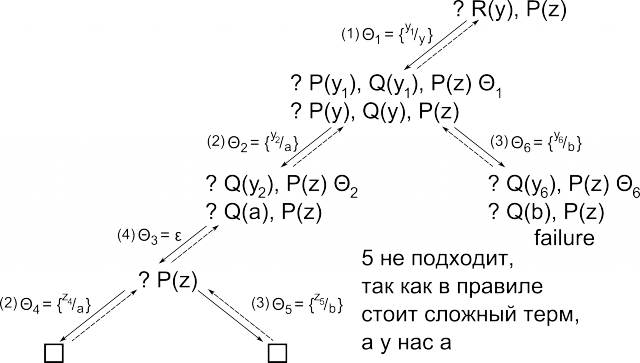Математическая Логика, 05 семинар (от 21 ноября)
Материал из eSyr's wiki.
Предыдущий семинар | Следующий семинар
[править] Логическое прграммирование
[править] Логическая программа
Логическая программа состоит из логических утверждений (правил) двух видов.
- A0 ← A1, …, An;, где левая часть (A0) — заголовок, правая часть (A1, …, An;) — тело, Ai = P(t1, tn), i = 0…n — правило. Имеет два способа истолкования:
- С точки зрения человека: если выполняются A1;, … ,An, то выполняется A0. Например, если записано P(x) ← P(f(x)), R(c), то оно трактуется следующим образом: «Если предмет c обладает свойством R и f(x) обладает свойством P, то x обладает свойством P»
- С точки зрения компьютера: чтобы решить задачу A0, необходимо сначала решить задачи A1, …, An. То есть, если интерпретировать предыдущий пример, то получим, что для решения задачи P(x) необходимо решить задачи R(x) и P(f(x))
- Программные утверждения второго рода — факты (такой способ принят в Прологе) Факт — правило без тела.
- Факты записываются следующим образом: A0 ← ;, где левая часть (A0) — заголовок; A0 — факт
- Интерпретация человеком: «я считаю, что A0 истинно»
- Интерпретация с точки зрения компьютера: «задача A0 априори решена»
Работа логической программы состоит в том, чтобы решить заданный набор задач (запрос, целевое утверждение). Вид запроса:
? C1, …, Cn
где C1, …, Cn — атомы, подцели.
- Интерпретация с точки зрения человека: при каких значениях переменных C1, …, Cn истинны (с точки зрения имеющихся утверждений)?
- Интерпретация с точки зрения компьютера: решить задачи C1, …, Cn, используя имеющиеся факты и знания
Как достигает этого компьютер?
[править] Простенькое введение в логическое программирование
Некий учёный хочет построить дерево родственных отношений для персонажей какой-либо книги (например, Библии). Для этого он читает Библию и вносит эти утверждения в программу. Интересны пол и имя. Вот, после нескольких первых строк учёный вносит утверждение:
Мужчина(Adam) ← ;
Теперь он (учёный) может обратиться с запросом:
? Мужчина('Adam')
то есть, является ли мужчиной Адам. Другой пример запроса:
? Мужчина(x)
то есть, все, кто является мужчиной. Учёный читает Библию дальше:
Женщина(Eve) ← ;
Потом возникают брачные отношения:
Муж(Adam, Eve) ← ; Жена(Eve, Adam) ← ;
Далее:
Отец(Adam, Abel)
После этого надо записать, что Авель — сын Адама, Евы, а также тот факт, что Ева — мать Авеля.
Через несколько страниц учёный попадёт в затруднительное положение, поскольку вносить надо всё больше. Но можно описывать не все связи, можно описать правила:
Сын(X, Y) ← Отец(Y, X);
«Если Y — отец X, то X — отец Y». Или, другими словами, чтобы проверить, является ли X сыном Y, надо проверить, является ли Y отцом X. Тогда:
Супруг(X, Y) ← Муж(X, Y); Супруг(X, Y) ← Жена(X, Y);
[править] Задача 1.1 (Родитель(X, Y); введение спецзаписи для нескольких альтернатив)
Как описать Родитель(X, Y)?
[править] Решение
Родитель(X, Y) ← Отец(X, Y); Родитель(X, Y) ← Мать(X, Y);
Для облегчения записи используется следующий трюк:
Родитель(X, Y) ← Отец(X, Y) |
Мать(X, Y);
[править] Задача 1.2 (Дед(X, Y); введение в теле правила дополнительных переменных)
Как описать Дед(X, Y)?
[править] Решение
Дед(X, Y) ← Отец(X, Z), Родитель(Z, Y);
Тут необходимо решить проблему введением нового объекта: переменная стоит в теле, но её нет в заголовке,тогда можно считать, что она связана квантором существования.
[править] Задача 1.4 (Брат(X, Y); введение встроенного предиката ≠)
Как описать Брат(X, Y)?
[править] Решение
Брат(X, Y) ← Родитель(Z, X), Родитель(Z, Y), Мужчина(X);
Достаточно ли полное это определение? Нет, получается, что я — брат сам себе: Брат(X, X) ← ; Тогда, для решения этой проблемы и полного описания необходимо описать предикат неравенства. Как это сделать? Можно считать, что человек идентифицируется по имени, тогда можно написать сравнение строк, сравнение букв (букв конечное количество, поэтому это возможно). Второй вариант — встроенные средства языка: X ≠ Y. Тогда полное определение Брат(X, Y) будет иметь следующий вид:
Брат(X, Y) ← Родитель(Z, X), Родитель(Z, Y), Мужчина(X), X ≠ Y;
[править] Задача 1.5 (Предок(X, Y); введения способа рекурсивного определения)
Как описать Предок(X, Y)?
[править] Решение
Предок(X, Y) ← Родитель(X, Y) |
Родитель(X, Z), Предок(Z, Y);
Вот Комсерг пишет, что Предок(X, Y) ← Родитель(X, Z1); …, Родитель(Zn − 1, Zn), Родитель(Zn, Y). То есть, что правило Предок есть транзитивное замыкание правила Родитель. Но это описывается рекурсией.
В каком порядке будет выполняться проверка? Согласно стратегии большинства интерпретаторов логических программ, утверждения выполняются в порядке их записи. Какие есть ещё варианты записи этого правила:
Предок(X, Y) ← Предок(Z, Y), Родитель(X, Z);
С точки зрения логики всё правилоьно. Но с точки зрения интерпретатора в данном случае откладываются отложенные проверки правила Родитель. Предыдущий способ описания является частным случаем рекурсии — итерацией. Тут же — чистая рекурсия.
[править] Домашнее задание (to be verified)
Задачи 1.3, 1.6
[править] Задача 1.3 (Быть_отцом(x))
Описать Быть_отцом(x)ф
[править] Решение
Быть_отцом(x) ← Отец(X, Y);
Существует Y такой, что X — отец Y
[править] Задача 1.6 (Родственник(X, Y))
Описать Родственник(X, Y)
[править] Решение
Родственник(X, Y) ← Предок(X, Y) |
Предок(Y, X) |
Предок(Z, X), Предок(Z, Y), X ≠ Y;
Далее — программные вещи.
[править] Структуры данных
Есть простые типы даннхы — строки, целые, …
Составные типы данных:
- В Си, Алголе, … основным составным типом является массив, отличительным признаком которого является произвольный доступ
- В Прологе, Лиспе основным составным типом является список, отличительным признаком которого является последовательный доступ
Список — более естественный тип данных с точки зрения рекурсии.
[править] Описание списка с точки зрения логики предикатов =
Есть nil — константа «пустой список»
Второй элемент, используемый для построения списков .(2) — двуместный функциональный символ, конструктор списков.
[править] Синтаксис списков
Списком является всякий терм (?), удовлетворяющий одному из двух правил:
- nil — список
- t1 . t2 — список, если t1 — любой терм, t2 — список
Пример списка: a . (b . (c . nil)))
Левый аргумент точки — заголовок, голова списка
Правый аргумент точки — хвост списка
Так как при написании списков приходится использовать скобки, а списки длинные и скобок тогда будет до чёрта, договоримся о правой ассоциативности точки.
Что такое (a . nil) . nil . nil
Если расставить скобки, то получим (a . nil) . (nil . nil), то есть, список из списка из элемента a.
Можно строить многомерные списки, деревья. Например, бинарное дерево: D1 . D2 . nil
Теперь решим две наиболее важные задачи в обработке списков:
- Написать программу, которая проверяет, что x является списком — list(x)
- Написать программу, которая проверяет, является ли y элементом списка x — elem(x, y)
list(nil) ← ; list(x . y) ← list(y); elem(x, x . y) ← ; elem(x, y . z) ← elem(x, z);
На примере второй программы рассмотрим, как работает интерпретатор. Рассмотрим, как выполняется запрос:
? elem(x, a . b . c . nil)
«что является элементом из списка (a, b, c)?»
Если имеется несколько подцепей, то он решает их по очереди.
Интерпретатор проверяет, подходит ли заголовок к подцели, то есть унифицируем ли он? При унификации переменные нормализуются (?).
- Унифицируем ли list(nil)? Нет, заголовки разные
- Унифицируем ли list(x . y)? Нет, заголовки разные
- Унифицируем ли elem(x, x . y)?
- elem(x1, x1 . y1) ← НОУ(x1, x1 . y1), elem(x, a . b . c . nil)) = {x1/a, x/a, y1/b . c . nil} = Θ1, то есть, унификатор существует.
- Далее применяется подстановка. Тело пустое, подзадачи кончились.
Какой результат? Результат — применение всех подстановок к подцели. То есть, {x/a}.
Но решений может быть много. Тогда интерпретатор откатывается на шаг назад и смотрит, найдутся ли другие правила. И они находятся:
- elem(x2, y2 . z2) ← НОУ(elem(x2, y2 . z2), elem(x, a . b . c . nil)) = {x2/x, y2/a, z2/a . b . c . nil} = Θ2. И тогда новая задача получается так: выбрасываем подцель, подставляем тело в начало запроса и образуем новый запрос:
? elem(x2, z2)
и, применим к нему Θ2:
? elem(x, b . c . nil)
Чтобы решить весь запрос, достаточно решить этот запрос.
- Унифицируем ли list(nil)? Нет, заголовки разные
- Унифицируем ли list(x . y)? Нет, заголовки разные
- Применяем третье правило: Θ3 = {x3/b, x/b, y3/c . nil} — унификатор нашёлся.
Выбрасываем исходную подцель, подставляем тело, применяем подстановку. В результате получили пустой список подцелей.
Что же будет подставлено вместо x? Θ2Θ3|x = {x/b} — b является элементом a . b . c . nil.
Быть может, есть другие варианты, откатываемся на шаг назад:
- 4 правило: Θ4 = {x4/x, y4/b, z4/c . nil}
? elem(x, c . nil)
- Θ5 = {x5/c, x/c, y5/nil}
Получили пустой список подзадач.
{x/c} — третий ответ на вопрос.
Откат на шаг назад.
Θ6 = {x6/x, y6/с, z6/nil}
Образован новый запрос:
? elem(x , nil)
3, 4 правила не подходят, унификатора не будет — в заголовке сложный терм с точкой, а у нас nil. Значит, failure, то есть неправильный порядок применений. Откат на шаг назад (backtracking), больше вариантов нет, …, откатываемся до корня и отвечаем, что получены три решения.
[править] Задача 3 (Построение дерева вычислений)
Построить дерево вычислений запроса G, обращенного к программе P.
G: R(y), P(z); P: 1. R(y) ← P(y), Q(y); 2. P(a) ← ; 3. P(b) ← ; 4. Q(a) ← ; 5. Q(f(x)) ← Q(f(f(x)));
[править] Решение
Ответ: Θ1Θ2Θ3Θ4|y, z = {y/a, z/a}, Θ1Θ2Θ3Θ5|y, z = {y/a, z/b}
[править] Задача 4.1
Выделить заголовок x списка L.
? head(L,x)
[править] Решение
? head(x . y, x) ← ;
[править] Задача 4.4
Построить конкатенацию (последовательное соединение) списков.
? concat(x,y,z)
[править] Решение
concat(x, nil, x) ← ; concat(nil, y, y) ← ; concat(x . x1, y, x . z1) ← concat(x1, y, z1);
[править] Домашнее задание
Задача 4.2, 4.3
[править] Задача 4.2
Выделить хвост y списка L.
? tail(L, y)
[править] Решение
tail(y . nil, y) ← ; tail(x . L, y) ← tail(L, y);
|
|
Ссылки
Официальная страница курса | Задачи
Проведение экзамена | Решение задач: Решение задач методички | Решение задач варианта экзамена 2004 года | Алгоритмы решения задач